首先需要理解什么是 "不含時(shí)"

在量子力學(xué)里, 對(duì)于單個(gè)粒子, 我們只關(guān)心它在哪個(gè)位置出現(xiàn)的幾率有多大, 而波函數(shù)在現(xiàn)實(shí)里是不存在的, 波函數(shù)只是恰好用來(lái)描述粒子非常好而使用而已

那么實(shí)際上我們關(guān)心的只是一個(gè)概率函數(shù), 用來(lái)描述粒子在某處出現(xiàn)的概率有多大, 并且這個(gè)函數(shù)也必定是實(shí)函數(shù),? ?而假設(shè) ψ(x,t) 是一個(gè)波函數(shù),? 那么? |ψ(x,t)|^2? 就恰好是我們關(guān)心的概率函數(shù)

"不含時(shí)" 的意思是說(shuō)概率函數(shù)不隨時(shí)間變化而變化,? 這就表明這個(gè)粒子找到了一個(gè)比較穩(wěn)定的狀態(tài).? ?? 而概率函數(shù)不隨時(shí)間變化而變化的話, 這時(shí)候我們也就可以假設(shè)對(duì)應(yīng)的波函數(shù)也不會(huì)隨時(shí)間變化而變化, 而且因?yàn)楦怕适菍?shí)值, 所以我們也可以設(shè)波函數(shù)是實(shí)值的, 但是看到原來(lái)的薛定諤方程, 里面有時(shí)間又有復(fù)數(shù), 很難想象怎么找到一個(gè)不含時(shí)的實(shí)值解,? ?所以為了描述 "不含時(shí)波函數(shù)" 我們需要不含時(shí)薛定諤方程

從含時(shí)變?yōu)椴缓瑫r(shí)

看到含時(shí)薛定諤方程:

我們的目標(biāo)就是根據(jù)一定條件求解里面的ψ(x,t)

而我們是假設(shè) ψ 與時(shí)間無(wú)關(guān)(不隨時(shí)間變化而變化),? 所以我們可以把ψ分成兩部分??ψ(x,t) = φ(t)*Φ(x) (分離變量法), 這時(shí)Φ就是我們需要的不含時(shí)波函數(shù)了, 但是, 單獨(dú)一個(gè)Φ是不符合薛定諤方程的, 所以這時(shí)候需要合適的變換:

把ψ= φ*Φ代入薛定諤方程中, 并且把微分無(wú)關(guān)的全部扔到微分外

然后兩邊同時(shí)除以ψ

可以看到方程的左邊只與位置x有關(guān), 方程右邊只與時(shí)間有關(guān), 這兩部分相等就證明左右兩邊應(yīng)該等于一個(gè)不與變量有關(guān)的常數(shù)

而推導(dǎo)含時(shí)薛定諤方程時(shí)就已經(jīng)知道:? ih*?Ψ/?t = EΨ,? 而現(xiàn)在等式的右邊就等于 E , 而E就是能量, 于是就有:

兩邊同乘Φ后:

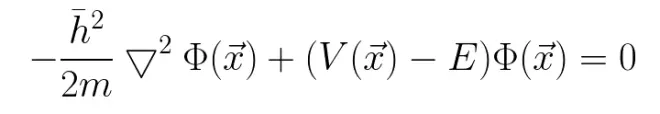
這個(gè)就是不含時(shí)薛定諤方程了

能量分立的原因

學(xué)過(guò)數(shù)理方程的人應(yīng)該可以一眼看出: 不含時(shí)薛定諤方程是S-L方程, 一定條件下必定存在分立解

但是為了照顧未學(xué)過(guò)數(shù)理方程的讀者, 這里舉一個(gè)例子:

在一維中, 勢(shì)V在0<=x<=1等于0, 其他地方等于正無(wú)窮? (一個(gè)非常簡(jiǎn)單的無(wú)限深井勢(shì))

然后我們來(lái)根據(jù)不含時(shí)薛定諤方程求解在這個(gè)勢(shì)中的波函數(shù)Φ

假設(shè)我們一開(kāi)始就知道 "粒子總會(huì)趨向勢(shì)低的地方移動(dòng)", 所以在[0,1]外的波函數(shù)必定為0, 就算我們一開(kāi)始不知道這個(gè)事實(shí), 數(shù)學(xué)也不會(huì)允許在[0,1]外的值不等于0的

而在[0,1]內(nèi)勢(shì)為0, 我們可以把勢(shì)V和不含時(shí)薛定諤方程一起寫(xiě)成比較簡(jiǎn)便的形式:

下面來(lái)求解 上面的式子:? ?稍微調(diào)整一下系數(shù)得

求解等式在高數(shù)里應(yīng)該也有給出的, 但是被指數(shù)函數(shù)洗腦的我有不同的見(jiàn)解(這個(gè)彎路繞得非常遠(yuǎn), 推薦忽略不看)

并且波函數(shù)必定是連續(xù)函數(shù) (只要粒子被觀察的一瞬間, 因?yàn)椴ê瘮?shù)坍塌才會(huì)形成不連續(xù)波函數(shù), 而觀察后也會(huì)馬上恢復(fù)連續(xù)), 在[0,1]外波函數(shù)值為0, 那么為了確保波函數(shù)的連續(xù)性, 有: ψ(0) = ψ(1) = 0

由ψ(0)=0 知道, A必須為0, 那么波函數(shù)變?yōu)?

已知B不為0 (B為0的話還玩什么啊), 那么有把ψ(1)=0代入:

解得:

歸一化: 概率函數(shù)的積分必須為1 (總概率為嘛....):

解得:? B=√2,? 于是波函數(shù)為:

其中, 對(duì)應(yīng)的能量為:

從上述過(guò)程可以看出,? 能量分立的原因是在解S-L方程中產(chǎn)生的, 而正是因?yàn)閿?shù)學(xué)是表達(dá)現(xiàn)實(shí)的方式之一, 所以事實(shí)上能量也確實(shí)是分立的

簡(jiǎn)單來(lái)說(shuō),?薛定諤方程表達(dá)了某種現(xiàn)實(shí)規(guī)律, 而求解薛定諤方程其實(shí)就算尋找符合規(guī)律的東西, 而在這里求解的結(jié)果就是: 只有能量取某些分立的值才能符合這個(gè)規(guī)律, 而不符合規(guī)律的能量也是不存在的