[Calculus] Heat Kernel
By: Tao Steven Zheng (鄭濤)
【Problem】
Verify that the normal distribution
satisfies the heat equation [1] (where
is a constant) for
, subject to the initial condition
, where
is the Dirac delta function [2].
[1] The heat equation is equivalent to
.
[2] The Dirac delta function is defined as

【Solution】
Take the first partial derivatives of with respect to
.
Take the first partial derivatives of with respect to
.
Take the second partial derivatives of with respect to
.
Thus,
Both sides of the equation match; therefore, the partial differential equation is satisfied.
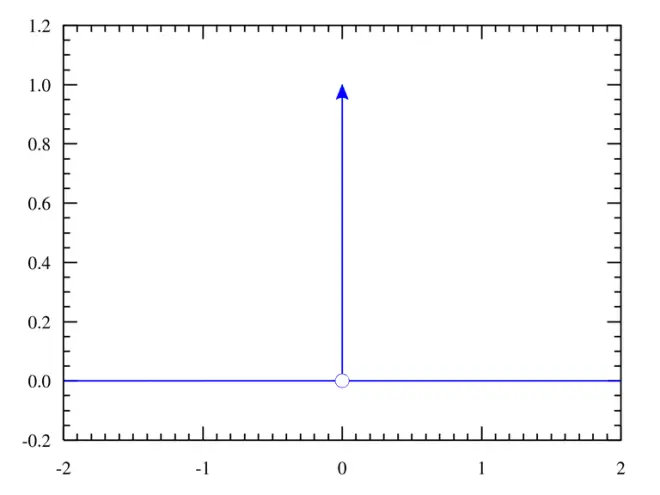
Now for the initial condition. The Dirac delta function is actually a distribution, not a function. In fact the limit
?
automatically verifies the validity of this initial condition.
標簽:

