ECON 159.?Game Theory

Lecture?06. Nash Equilibrium: Dating and Cournot

https://oyc.yale.edu/economics/econ-159/lecture-6

Last time we were talking about The Investor Game and this was a coordination game.?One thing we learned was that communication can help in a coordination game. Our Jimmy Stewart character and helped coordinate you on a better equilibrium simply by suggesting what you should do.?

There are two lessons here. One is this is very different from the Prisoner's Dilemma. So we learned the very first time that in the Prisoner's Dilemma communication per se won't help, but in the coordination problem, which could be just as serious socially as a Prisoner's Dilemma, in a coordination problem it may well help. The reason it helps is you're trying to coordinate onto a Nash Equilibrium. One way to think about Nash Equilibria is that they are self-enforcing agreements, so provided that everyone believes that everyone is going to go along with this agreement, then everyone in fact will.?

I want to make another, slightly more philosophical remark associated with this and it's to do with the idea of "leadership."?I don't think Game Theory is going to contribute to anything to understanding about leadership. But one thing we can do is tell you where leadership may help. In the coordination game, where the idea is to try and get people to coordinate on a particular equilibria rather than on another equilibria, or worse still, to be uncoordinated entirely. In those kind of games, a?little bit of leadership can help tremendously. So these games, these coordination games, are games where there is a "scope for leadership."?

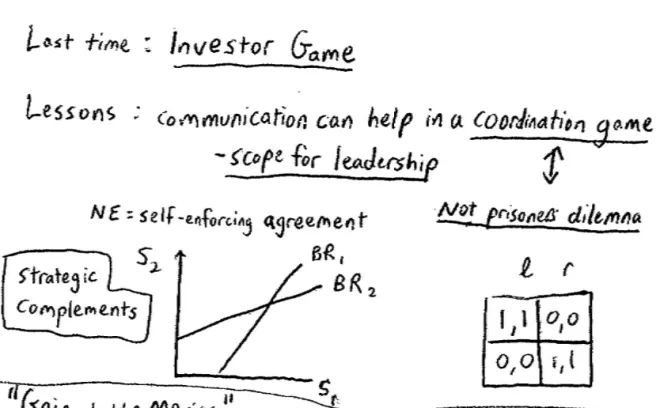
Just to see that in a very simple example, again, we don't use such a complicated example as the one we looked at last time, you could imagine a game, a really trivial coordination game, which looked like this (1,1) (0,0) (0,0) (1,1). And clearly in this game what matters is coordinating. You either want to coordinate on up left or you want to coordinate on down right. You don't want to end up uncoordinated on down left or up right.?

In that game, if you remember what the best responses looked like, they looked like this where this was the effort of Player 1; this was the effort of Player 2. This was the best response of Player 1 and this was the best response of Player 2. This game also has the feature that the more effort the other person?does,?the more you want to do. The more effort your partner provides into this project the more effort you want to provide in this project.?These games in which the more the other person does the more I want to do, these are called games of strategic complements. These are games of strategic complements. So both the investment game and the partnership firm game are games with strategic complements.?

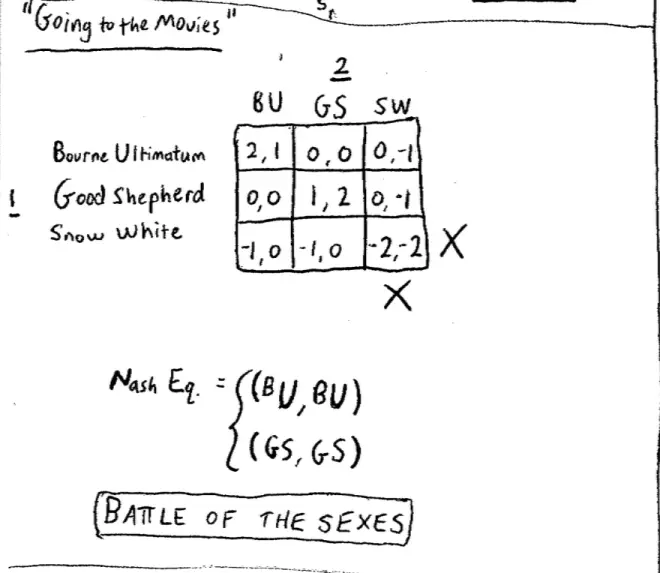
We'll look at and play another game, "Going to the Movies." The movies we're going to look at are?The Bourne Ultimatum, and the movie called?Good Shepherd, and a movie called?Snow White?and I'll explain the game in more detail in a second.?So let's put the payoffs in here. So the idea here is that these people are going to meet at the movie, they're going to go out to a movie. But?they have forgotten to tell each other which movie they're actually going to go to. They're going to meet in there in the back row probably.?

So here we go so … -1,( -1, 0), (-1, 0), (-2, -2). So here are the preferences for these movies of Player 1 and Player 2, and you can see from these preferences, from these payoffs, that the best thing for Player 1 is for both players, both people to meet and go to the?Bourne Ultimatum; this is the action movie. And she gets nothing if they fail to coordinate and so on and so forth. Her second choice is to manage to coordinate at Matt Damon being a Yale spy, and then she really doesn't want to go and see?Snow White, and the worst thing of all, actually this is for both players, the worst thing of all is to coordinate with?Snow White.?Same thing with the other person. Same thing exactly, except that he would rather meet at the?Good Shepherd.?

So now, that was good, we managed to coordinate. I think we can all see that we might not have done. Let's try some communication in this game. We said that coordination games are helped by communication. For some reason it was cancelled that night because someone had a bad cold or something. You are about to go off on Friday night to see these movies and let's allow some communication ahead of time.?

The Nash Equilibria?are both people doing?The Bourne Ultimatum?or both people doing?The Good Shepherd.?Unlike the other game, the two examples of coordination games we saw so far were really pure coordination problems.?There was no conflict at all. In the case of the Investor Game last week, every player preferred one equilibrium to the other. The game I just put up, that's a trivial example, it didn't really matter which equilibrium we played here, we just wanted to play an equilibrium.?But here, there's a potential source of conflict here. Both people would rather be at an equilibrium than to be mal-coordinated or uncoordinated, but Player 1 wants to go to?Bourne Ultimatum?and Player 2 wants to go to?Good Shepherd, and actually I thought Nina's strategy there was pretty good. Nina's version of communication was, "I'm going to?Bourne Ultimatum." That basically fixed things.?

But you could imagine that communication could break down here. There could be a negotiation going on. There was a critical moment this morning up in Detroit between General Motors and the united autoworkers and I don't want to say that strikes are only about mis-coordination, but clearly, everyone's better off if they come to some agreement rather than strike. There's at least some agreement that's going to be better for everybody than a strike, and yet, because they're conflicting interests there, basically in that case conflicting interest about health and pension payments, it could well be that you end failing to coordinate.?

So this game's called The Battle of the Sexes and we'll see it in various forms over the course of the semester.?Games like it, they are coordination games but different people disagree about where you'd like to coordinate.?

We're going to spend most of the rest of today talking about Cournot Duopoly. Now, as a purely Game Theory exercise, one reason for studying Cournot Duopoly, is that so far we've discussed how to find Nash Equilibrium when there are few players, each of whom has few strategies, and we've discussed how to find Nash Equilibrium where there are many players, each of whom has few strategies, and this is a game where there are few players, maybe two, but they have many strategies. They actually have a continuum of strategies.?

This is a game in which there are two firms who are competing in the same market. One reason this game is interesting from the point of view of economics, is this game lies between the two extreme cases that you learn about in your Intro Economics class. One extreme case is perfect competition and the other extreme case is monopoly. So this is really the first attempt, way back in the nineteenth century to study a market that's somewhere in the middle, where it happens most markets are--there are two firms.?

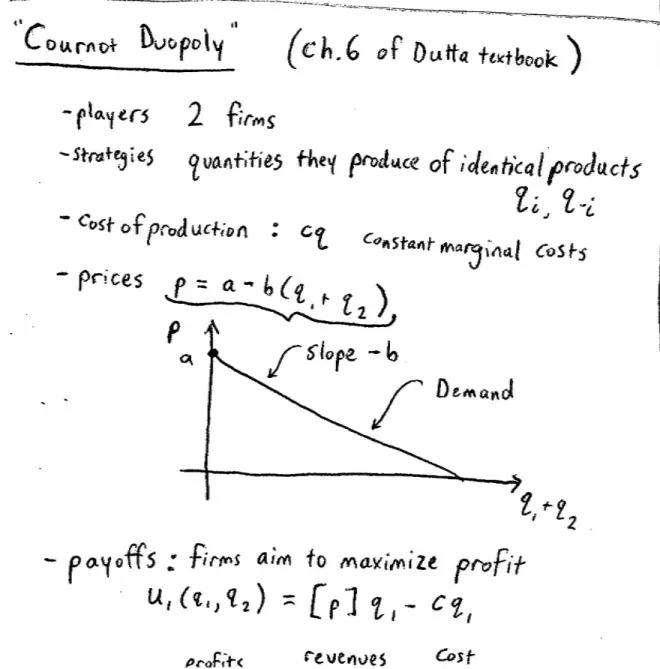
So the players in this game are two firms and the strategies are the quantities that they produce of an identical product. So they are the quantities they produce, each of them produces, of an identical product. So as far as the consumers are concerned, these two products are perfect substitutes.?So qi and q-i or q1?and q2?will be the strategies.?

We need to give a little bit more structure on the payoff before I get to the payoffs. So in particular, I need to tell you what is the cost of production. And the cost of production in this game is simply going to be cq.?This a setting in which we have constant marginal costs,?c.?

So prices are determined as follows:?the more these firms produce, so the more the total quantity produced q1?+ q2, the lower is the price in the marketplace for this product. So this equation I've just written, if you can imagine q1?+ q2, total quantity on the horizontal axis, and you could imagine price on the vertical axis, and basically what we're saying is that prices depend on total quantities as follows: where the slope of this line is -b.?It's a demand curve. It tells me the quantity demanded at any given price.?

So payoffs for these firms are going to depend on profits. The firms' aim to maximize profit and the payoff for Firm 1, as it depends on the quantity that she produces and the quantity that the other firm produces, is going to be prices times the quantity that Firm 1 produces minus costs times the quantity that she produces. So this is--this term here is revenues and this term here is total costs. Revenues minus costs makes profits.

What I'm going to do here is I'm going to substitute in for prices. So I've got this expression for prices here, here it is, and I want to plug it into that P there. And I'm going to rewrite it now with that P expanded out. So I'm going to get--I'm going to multiply it out at the same time, so I'm going to have aq1?- bq12 - bq1q2?- cq1.?So here I have a new expression for Firm 1's profit and I could do the same for Firm 2.

Both firms are producing quantities; both firms are trying to maximize profit, and I want to find out the Nash Equilibrium. Identify the best responses of each player as a function of the others and find out where they intersect.?What we're going to do is we're going to figure out Player 1's best response quantity to each possible choice of Player 2, and then we're going to flip it around and figure out Player?2's best response quantity to each possible choice of Player 1, and then we're going to see where they--where those coincide, where they cross.?We're going to differentiate with respect to q1, the thing we're trying--our control variable, the thing we're trying to maximize the thing with respect to and set it equal to 0.?

So this term here aq1?is going to become an a and this term here -bq2 is going to become a 2bq1?and this term here, -b q1q2?is going to become a -bq2, and the last term -cq1?is going to become a -c. What I did was I differentiated this fairly simple function with respect to q1?and since I want to find a maximum, what I'm going to do is I'm going to set this thing equal to 0. At my maximum, I'll put a hat over it to indicate this is the argmax; at my maximum I'm going to set this thing equal to 0. This was a first order condition or a first order necessary condition. I actually need to check the second order condition.?

So how do I check the second order condition??I differentiate a second time and check the sign, so the second order condition, I differentiate this expression again with respect to q1. The only place q1?appears here is here, so when I differentiate again I'm going to get -2b and sure enough that's negative, which is what I wanted to know, just to check that when I'm finding this thing, I'm finding a maximum and not a minimum.?

So what I have here is an equation that tells me Player 1's best response for each possible choice of Player 2. I could do the same thing for Player 2 to find Player 2's best response for every possible choice of Player 1.?

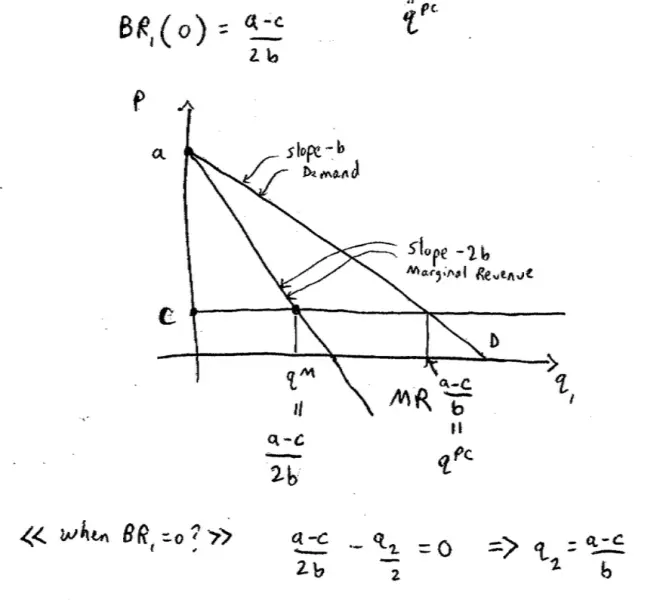
If I plug q2?= 0 into here, this term disappears and I just get a - c over 2b. What's that telling me? Let me put the 45o line in here. What's that telling me is that if Player 2 chooses not to produce then Player 1's best response is a - c over 2b. Now, I claim that that quantity, a - c over 2b actually has another name.?If Player 2 is producing nothing, then what is Player 1 effectively? He's a monopoly; so she's a monopolist, so we know how to figure out monopoly quantities.?It's where the marginal revenue is equal to the marginal costs.

What's the marginal revenue look like in this picture on the left? It's twice the slope but that's fair enough.?So the marginal revenue here,?the monopoly quantity is when marginal revenue equals marginal costs. As we know, this line here has twice the slope of the original line of the demand curve, so the slope of this thing is -2b.?

Now, I'm going to claim that this monopoly quantity I claimed before is going to--our intuition says if the other firm isn't producing, my best response must be to produce monopoly quantity which I can see on this picture that quantity is a - c over 2b.?How can I see they're the same thing? Well look, here I have a line of slope -2. How far down does it have to go? It has to a - c down. This pink line has to drop off from a all the way to c. How far along do I have to go drop off a - c when I have slope -2b? Answer a - c over 2b.?So this monopoly quantity is indeed a - c over 2b.?

How much quantity would Firm 2 have to produce in order to induce Firm 1 not to produce at all? It is?a - c over 2b.?That's just solving out the algebra, so what q solves, a - c over 2b - q2?over 2 = 0. What q2?makes this equal to 0 and Katie's answer is solving out the algebra here is that q2?that solves this must be a - c over b.?

Let's go back to the economics. So I'm claiming that there's some quantity up here. I claim this quantity is a - c over b such that if Firm 2 produces that much quantity, Firm 1 will just produce nothing.

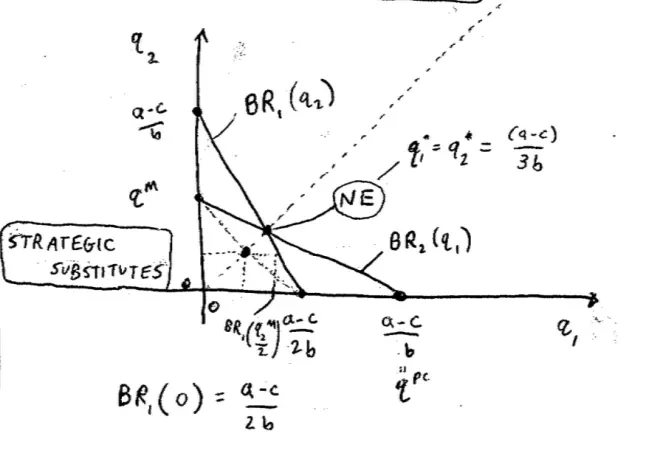
What quantity, if produced by Firm 2, would cause Firm?1 to shut down on this picture??That's where the marginal cost and the demand thing, demand lines intersect. So?if Firm 2 produces all the way up to here then any product produced by Firm 1 is going to push prices even lower. In particular, they'll be lower here than costs and so you'll make losses on that product. what's the name for this quantity? The quantity where demand and marginal costs equal--that's the competitive quantity. So this is the perfect competition quantity. In a perfectly competitive market that's exactly where prices are going to end up. This is not a perfectly competitive market, but if it were, that's where price is going to end up.?

So this is Firm 1's best response as a function of q2. What is Firm 2's best response as a function of q1??It's symmetrical across the 45o axis. What's the Nash Equilibrium on this picture? It is?where the green and the pink line intersect. Why is this the Nash Equilibrium? Because at this point, as in the partnership game, which there was a similar thing, as in the partnership game where the best responses intersect is where Player 1 is playing a best response to Player 2, and Player 2 is playing a best response to Player 1. So this is the Nash Equilibrium in this Cournot game.?

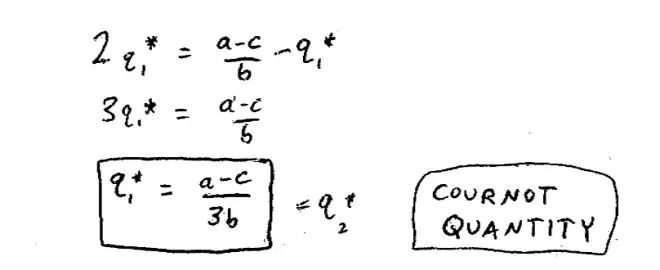
So at the Nash Equilibrium quantities I'm going to have q1* is equal to a - c over 2bq* and q2* is equal to a - c 2bq1* over 2 and now we're going to solve this out by setting q1?= q2?since I know the game is symmetric and they were on the 45o line.?So putting q1?in here--if I substitute q1?in here, what will that give me? It'll give me q1* is equal to a - c over 2b - q1* over 2. Let's multiply both sides by 2, I'll get 2q1* is equal to a - c over b - q1*. I have 3 q1* is equal to a - c over b; and finally divide by 3 q1* is equal to a - c over 3b. So that crossing point actually occurs at a - c over 3b. I'm going to look desperately at my T.A.'s to make sure I didn't screw that up. So this is something that's called the Cournot quantity.?

Now, this game, this game of imperfect competition between two firms competing in quantities, was thought up and studied by a French economist called Cournot almost a hundred years before Nash. So a hundred years really before the invention of Game Theory, someone had figured out this answer for this game. Okay, so what do we know so far? I'll leave the algebra there, transfer it up here, q1* = q2* = a - c over 3b.?

It's different from the partnership game, it's different from the investment game. What is it that's different about this game from the--what's the obvious thing just looking at this picture that makes it different from the partnership game? In the partnership game the best response lines sloped up. The more I did of my strategy, the more the other player did as a best response. In the investment game, the more likely I was to invest, the more likely you--the more you wanted to invest.?

But in this game we have the exact opposites. The more Player 1 produces, the less Player 2 wants to produce and the more Player 2 produces, the less Player 1 wants to produce. So this game is a game, not of strategic complements, but of strategic substitutes. It's not that these goods are substitutes.?If both these firms are producing bottled water and it's identical, then the goods themselves are substitutes. That's not the point I'm making here. Strategic substitutes is a statement about the nature of the game. So strategic substitutes is telling me that my strategy is a strategic substitute of your strategy if the more I do at my strategy, the less you want to do of yours and conversely, the more you want to do of your strategy, the less I want to do of mine.?

Now, let's come back to the question we started with, which has to do with profits and so on in society. We know that if these players play these games, at least if we believe in Nash Equilibrium, then they're going to produce these quantities, they're going to produce here. But let's ask a different question.; Each of these firms is trying to maximize profits, but how about the total profit in the industry? Total industry profits are not being maximized. Where on the picture--let me do a bit more cold calling here--where on the picture maximizes total industry profits? Monopoly, exactly.?

So clearly, if we produce the monopoly quantity, by definition, the monopoly quantity maximizes total industry profits. For example, if Firm 2 shut down and Firm 1 produced its monopoly profits, that is, a monopoly quantity, that would maximize firm profits. Conversely, if Firm 1 shut down and Firm 2 produced its monopoly quantity that would maximize industry profits. Where else in this picture maximizes industry profits? So this point maximized industry profits and this point maximizes industry profits. Where else maximizes industry profits?

Well, how about all the points in between? Here, Firm 1 produced nothing and Firm 2 produced a monopoly quantity; and here Firm 2 produced nothing and Firm 1 produced a monopoly quantity. But you could also just split the monopoly quantity, for example, half half at this point here. So if the firms wanted to make more money, the only thing they could do is they could sign an agreement saying, why don't each of us produce not our Cournot quantity, but produce half the monopoly quantity and that would produce this much each. So Firm 1 would be producing half its monopoly quantity and Firm 2 would be producing half its monopoly quantity.?

So what's wrong with that agreement??It's illegal. So even without there being an Attorney General, somebody might be awake in the justice department and notice that that's actually illegal. It's illegal to sign an agreement?to sign a contract saying you're going to restrict quantities.?

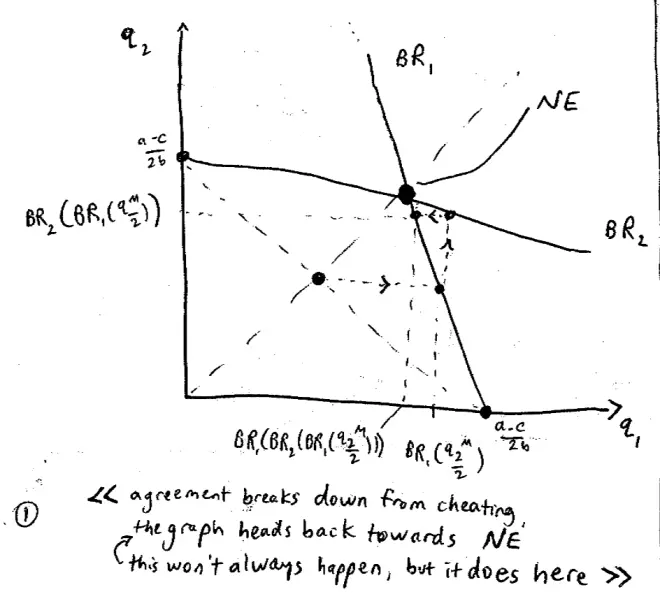
It's illegal, so they can't sign that as a contract, but they they can just agree to do it. But company A's?best response to company B?producing the monopoly quantity?is to overproduce relative to the monopoly quantity, actually overproduce even relative to the Cournot quantity and produce all the way out here.?

So?anticipating that company A?is going to cheat and?produce too much, B is?going to produce a best response to that and he's going to produce this quantity here. So what is this? This is Player 2's best response, so Player 1's best response to Player 2 producing half monopoly output.?

This is the best response of Player 1 to the best response of Player 2, to the best response of Player 1 to Player 2 producing half monopoly output and there are lots of brackets here. Can anyone see where this process is going? It's going back to the Nash Equilibrium. Each of them is trying to play a best response for what they anticipate the other person's going to do. And in this game if they keep on doing that, it's going to drag them back to Nash Equilibrium. But in this game, playing best response to each other, figuring out that in fact the other guy is going to cheat on me, or the other guy is anticipating that I'm going to cheat on him, or the other guy is going to anticipate that I'm going to anticipate that he's going to cheat on me, etc., etc., will eventually drag us back to the Cournot quantity.?

So it's going to be pretty difficult for us to sustain this joint monopoly output, this collusive agreement. We can't let the courts enforce it. We're Coca-Cola and Pepsi, so we really don't want to have to bring the mafia in, although maybe we do, I don't know. So basically, we're stuck with this verbal agreement and we both have an incentive to cheat and produce more whatever it is, sugar water.?

Now, in practice, this is not the only problem facing two firms who are trying to produce the monopoly output. In practice, when firms try and have these agreements, which are not contracts, to try and produce joint monopoly output, what else goes wrong? So you can imagine some firms trying to have an agreement. We know they can't sign a legal agreement, but let's take that off the table. So, for example, in around 1900 in America or a little bit earlier, let's say 1880 in America, it really isn't clear that it was illegal to write agreements to say we'll restrict quantities. So firms did use to write that kind of agreements, but still something went wrong. What went wrong? So we're getting a little bit further away from the game and more back into the real world.?

Another firm is going to come in and produce a similar product. So Dr. Pepper or something, is there one? Someone else is going to come in and produce cola in this industry and that's exactly what happened in the U.S. at the turn of the last century. Companies did produce agreements to restrict, for example, the production of paper and the production of rubber, and the production of steel, and the production of iron, and the production of railway lines, actually, even quite complicated things. Sure enough what you see very quickly emerging is new entrants entering the market to say, hey these firms are restricting their quantities, we can get in there and make money. So new and a competitive fringe of firms is going to enter and drive prices down.?

Now, I'm talking about 1900 America where has that happened in the twentieth century more dramatically? We know the early example in sort of Golden Age America, but where else did we see a competitive fringe enter when there was a collusive agreement to keep quantities down?

Oil is probably the classic example. So in oil we all know that in the late 60s, early 70s, OPEC was formed precisely to restrict quantity among the major oil producing countries, and very quickly we see companies take--other countries take advantage of this to start producing oil profitably. So who were the competitive fringe against OPEC??The Brits were for a start, the Brits--England sort of--Scotland I should say. Britain anyway started producing oil in the North Sea; lots of countries in Latin America started looking and finding oil, and of course, Russian oil started being very, very profitable.?

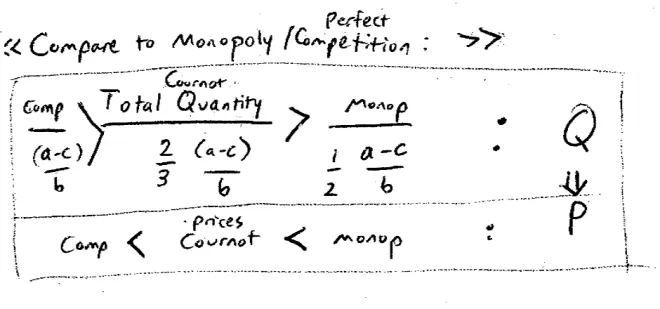
So there are various reasons why it's hard to maintain this collusive agreement. One is there's an incentive to cheat and another is that other firms are going to enter.?Suppose, in fact, we do end up back at the Cournot quantity. So here we are back at the Cournot quantity. How does this quantity compare and how do therefore the prices compare, and how do profits compare with monopoly prices on the one hand, and competitive prices on the other? So we know the quantity that's going to be produced.?We know the quantities going to be produced. Each firm is going to produce a - c over 3b and there are two such firms. So the total quantity produced in the market--the total quantity will be 2a - c over 3b.?

How does that compare to the monopoly quantity? Well, the monopoly quantity was a - c over 2b and the competitive quantity was a - c over b.?So this is the total quantity produced on this equilibrium, in this Cournot Nash Equilibrium. How did it compare to the monopoly quantity and to the competitive quantity??

So I claim that this total quantity being produced is less than the competitive quantity, but more in total than the monopoly quantity.?Total quantity being produced is less than would be produced under perfect competition, but more than would be produced under monopoly. Consequently, prices are going to go the other way and consequently prices are going to be highest under monopoly, lowest on the competition, and somewhere in between in this Cournot situation.?

So from the point of view of the producers, this Cournot Equilibrium is worse than monopoly, but better than perfect competition. And from the point of view of the rest of us, the consumers, this Cournot quantity is worse than perfect competition but better than monopoly.?