ECON 159.?Game Theory

Lecture?08. Nash Equilibrium: Location, Segregation and Randomization

https://oyc.yale.edu/economics/econ-159/lecture-8

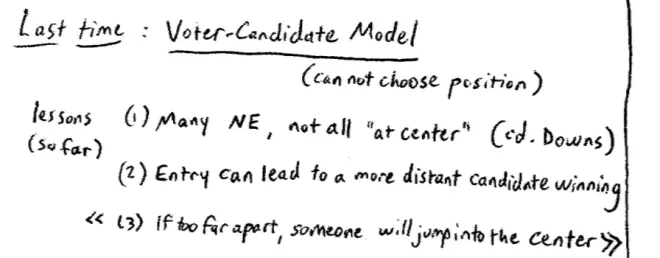
Last time we left things in the middle of a model, which was the candidate-voter model. The main thing that was different was that the candidates cannot choose their positions. If you like, every voter is a potential candidate but you know the positions of the voters.?

The first lesson is there can be lots of different Nash Equilibrium this model. There are multiple possible Nash Equilibrium in this model and more to the point, not all of those equilibria have the candidates crowded at the center. We saw early on in the classic Downs or median-voter model that that model predicted crowding the center. This one doesn't.?And a second thing we saw last time was that if you enter on the left one affect of entering on the left can be to make the candidate on the right more likely to win. Conversely, if you enter on the right--you're a right-wing voter candidate and you enter, that can make it more likely that the left wings are--can lead to the winner being more--being further from your ideal position.?

The person in the center could stand up and win. Actually, it doesn't only have to be the person exactly in the center. A wide array of center candidates could deviate and win at this point. So, if this was the two candidates standing, and you imagine a third candidate standing who is??a little bit closer to the center,?fairly clearly he's going to end up winning. So this is the third lesson. If the candidates are too far apart we're going to see some center entry, which is going to win.?So even though there isn't this full Downsian effect of pushing candidates towards the center, even though we don't have the median-voter theorem here, we still have part of the intuition surviving. The part of the intuition that's survives is, if the candidates are too far apart, then the center will enter and win.?

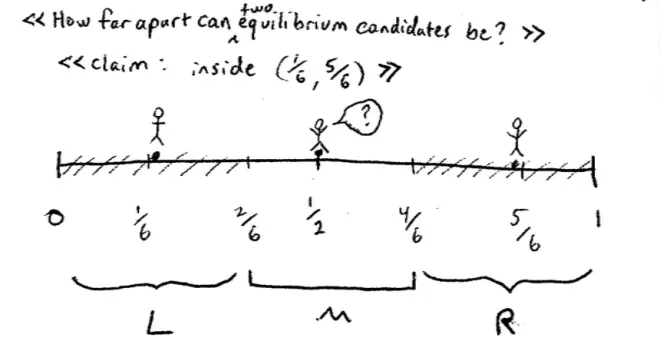
So a reasonable question here is just how far apart in equilibrium can the candidates be??

Here's the full extent of our political spectrum from 0 to 1, and let me just try and illustrate how far apart these can be. What I'm going to do is I'm going to divide this into sixths - 1/6, 2/6, 1/2, 4/6, 5/6. So I claim--and I'll show afterwards--I'll claim that provided the two candidates aren't outside of 1/6 and 5/6 that that will be an equilibrium. So, in particular, if the candidates are just inside 1/6 and just inside 5/6, or just more than 1/6 and just less than 5/6--so here's one of these candidates who's standing and here's the other one.

What are they vulnerable too? They're vulnerable to deviation by somebody entering at the center. And if somebody enters at the center--what would make somebody enter at the center? They're going to enter at the center if they can win basically. So if they enter at the center in this case, let's see how many votes everyone gets. So if we enter at the center here--here's our new candidate--who's thinking about entering at the center. So he's sort of thinking about it. So what's his or her calculation going to be? Well, let's look at what would have happened. So all of these voters are going to vote for our left-wing candidate. So these are going to vote for the left-wing candidate. All of these voters are going to vote for the right-wing candidate. They're all closest to the right-wing candidate. And the middle third--that's a third of the voters, another third--and the middle third (these ones here) are going to vote for the center candidate.

So I've basically divided--the reason I divided it into sixths is I want to put everybody at the middle of a third. So here the left-wing candidate is at the middle of the left third; the right wing candidate is at the middle of the right third, and the center candidate is at the middle of the center third not surprisingly. So if the center candidate enters, if they were exactly at 1/6 and 5/6, they would split the vote and the center candidate would win with probably 1/3. But without worrying about that exact case suppose that this--as I claimed that the left-wing candidate is just slightly to the right of 1/6 and the right wing candidate is just slightly to the left of 5/6. Now this left-wing candidate gets a few extra votes here and the right wing candidate gets a few extra votes here?and you can see now that the center candidate isn't going to win. Because the left-wing candidate is getting slightly more than 1/3 of the votes; the right wing candidate's going to get slightly more than 1/3 of the votes; so the center candidate is going to get squeezed out.?

So the third lesson here is if the candidates--if the two candidates are too extreme--where too extreme in this model meant beyond… meant less than 1/6 and more than 5/6--but are too extreme, someone in the center will enter.?

Again, if you look back in both American History and other countries' history, you'll see that when candidates are perceived to be too far apart there's been tremendous temptation for center parties with third parties to establish themselves in the center. So again, with some biased towards England, this is what happened in English History during the Thatcher Period for example. The Thatcher government was perceived to be quite far on the right. The Labor Party at times could be quite far on the left. And we saw a center party set up in between them.?

There's a also a Game Theory lesson that I want to just keep in mind here without--well, there's a Game Theory lesson here. And the Game Theory lesson is that our method of finding equilibrium in this model, which was what--it's guess and check--is actually pretty effective. You might think that guess and check, since it doesn't sound like advanced mathematics, wouldn't be such a great way of going about solving games and thinking about them, and thinking about the real world. But actually, guess and check did pretty well here. We were able to make sensible guesses pretty quickly. We were pretty quickly able to figure out what was going on.?

And the key here is what? Without writing it necessarily, the key here is: be systematic when you're guessing. Make sure you've looked everywhere. And second, be systematic, be careful when you're checking. The big error is to ignore certain types of deviation. In this particular model, people very quickly realized that one possible deviation is for someone else to enter. But perhaps they're a little bit less good at spotting that another possible type of deviation is for somebody to drop out. You want to look at all possible types of deviation. But if you're careful, this is a very effective method. So, that's all I want to say about this politics model, and I want to move onto a model that perhaps has more to do with sociology. We'll do a little tour of the Social Sciences here in showing how Game Theory can apply to each in turn.?

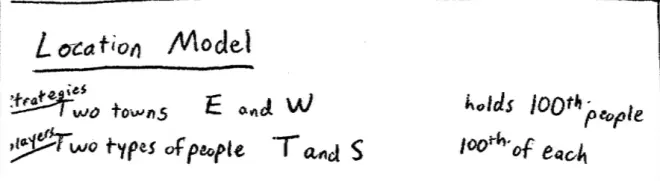
So, we're going to play another game this morning.?It's going to be another location model, But the idea of this game is as follows. We're going to imagine that there are two towns, two possible locations, and we'll call them East Town and West Town. And we're going to assume that there are two types of people in the world,?tall and short.?

The idea here is that people are going to choose where they live. Let's assume that there's lots of people. there's 100,000 of each type of person. And let's assume that each town holds 100,000 people. These are fairly big towns. So, the players in this game are going to be the people, the 200,000 people--200,000 tall people and 200,000 short people--but in a minute I'm going to tell you whether you're tall or short. The strategies are going to be a choice of whether you choose East or West. So these are the players and these are going to end up being the strategies.?

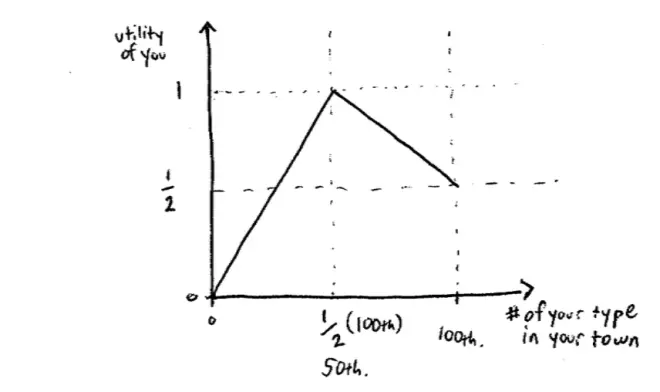
To model the payoffs, let me first of all draw a picture. On the horizontal axis I'm going to put the number of people of your type in the town you end up in. So on the horizontal axis is the number of your type in your town. So the most this could possibly be is 100,000 because that would say everybody is the same type as you in the town and the lowest it could possibly be is 0 because that would say that everyone in the town except for you is of the other type.

The idea is, if you are a minority of 1 in your town, so everyone else is of the other type, you get a payoff of 0. If you are in the majority, and in fact, everyone in your town is of the same type then you get a payoff of a 1/2. If it's the case that your town is exactly mixed, so half of your town is tall and half of your town are short, then you get a payoff of 1. I put a half here. That's really the wrong thing to put here, it should be a 1/2 of 100,000 so I guess it's 50,000. So if it's the case that 50,000 of the people in the town are your type and 50,000 are the other type, then you get the highest possible payoff which is 1.?

They'd like to live in mixed towns, but if the town is not--if they had a choice between two towns and the towns are not evenly mixed, then theyd prefer to be in the majority town-- the town in which they're the majority.

So to play this game, I need to put down a few more rules. So the first rule is going to be that the choice is simultaneous and that's a little unrealistic because in practice, of course, people choose their towns sequentially, wherever they happen to be moving, but for the moment let's leave it as that. Second, I need to just say what happens if too many people choose the same town. So if there's no room in a town, for example, if too many people chose East Town then we allocate the surplus randomly. We ration the places randomly. So then--we then randomize to ration. For example, there's 100,000 places in East Town, so if 150,000 people chose East Town, you're going to have a 2/3 chance of getting into East Town and the rest of you is going to be allocated to West Town.?

Why did we end up like that? How did we end up like that? We started off with a stripy pattern. It was a little bit off from being kind of perfect, because all of you, by these preferences would prefer to be in a town that was exactly 50/50. It wasn't quite at 50/50 but it wasn't far off actually and we pretty quickly ended up with all these short people, you guys are short all living in East Town and all of you all tall people living in West Town. So all of you pretty much ended up with a payoff of 1/2. Some of you didn't, there are a few deviants. The?deviants are those?tall guys who end up East Town? They end up with a payoff close to 0. And who are my short deviants who ended up in West Town? There's a few. Not many of them at all actually, but a few of them, but they end up with a payoff of 0 as well. But pretty much everyone else was ending up with a payoff close to a 1/2, and splitting down the middle of the room. What do we call that process? What's the outcome here??

So this is segregation. Right, we ended up getting the class to segregate on tall and short. It wasn't that people wanted to segregate. I gave you the preferences. I told you that you have to have these preferences, which may have actually been the preferences that favored being in a mixed town, but we very quickly settled down to a segregated distribution of the class.?

So what's an equilibrium of this game??Everyone being segregated. There's three ways to be segregated and each of them seems like an equilibrium. So all the tall people being in the East is one equilibrium, and all the tall people being in the West is the other equilibrium. Both of those?are Nash Equilibrium. How do we check that they're Nash Equilibrium? ?You check for profitable deviations.?A?deviation is for one of the short guys to move to West Town.?At the equilibrium that short guy was getting a payoff of what? What was his or her payoff in equilibrium? One half. If he or she deviates and moves to West Town, again ignoring the capacity constraints, let's assume that they can, if that short person moves to West Town what's their payoff going to be? Zero. So that's not a profitable deviation. Conversely, if we did the same from the other side for the tall people, we'd find the same thing. So we've just checked that that is an equilibrium because nobody can deviate profitably. So we found two equilibria here and as people pointed out they are segregated.

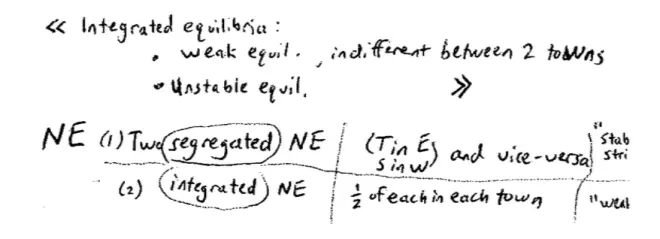
If the crowd had split 50/50 that would also be an equilibrium. If people split exactly 50/50, right split the class down the middle--I start off by splitting it this way into tall people and short people--if I had split the town down the middle into East and West, then everyone would have been happy and they would have stayed put. But?It's a weak Nash Equilibrium because while there's no real incentive for you to deviate, there's no incentive for you to not deviate either.?What do we mean by that? If we deviate away from this exactly mixed equilibrium, roughly speaking, a little bit of hand waving here, but roughly speaking we're exactly indifferent. It's true, that's not strictly true because I guess by ourselves moving we're changing the balance a little bit, but nevertheless we know if I smooth out the top it'll we'll be exactly right.?

So at that integrated equilibrium, I'm exactly indifferent about where I live, both towns look the same to me. They're called East and West but they have the same mixture of tall and short people in them. Whereas, at the segregated equilibria, I strictly prefer to go to the town in which I'm the majority. I'm doing a strictly higher payoff, 1/2 versus 0, by being in the town in which I'm in the majority. So there's this notion of strictness, there's also a notion of stability here, so again, I don't want to be too formal here. I want to give you an informal idea about why we might worry about stability. So what do I mean by stability here? Why do I think that that integrated equilibrium in which we divide the towns equally might not be stable? What do we mean by that? For the physicists this is an easy idea, but for everyone I think it's a fairly intuitive idea. Why is that not likely to be stable? Anybody? Yeah here. What's your name?

So at that integrated equilibria, if we move away from it a little bit, if it turns out that, let's say, one town has 5% more short people and the other town has 5% more tall people, then in some sense we're in trouble already. We haven't gone very far from this nice equilibrium but already we're in trouble because now all of the short people are going to prefer East Town and all of the tall people are going to prefer West Town. And in a few moves we're very quickly going to be back at segregation again. It's not stable in the sense that if we were a little bit off we're going to go a long way off.?

So the Nash Equilibrium in this game--we have two segregated Nash Equilibria and these correspond to tall in East and short in West and vice versa. We had a separate one which was an integrated one which was roughly half of each in each town. So there's at least three equilibria here, although the two segregated ones are kind of the same, and we argued that these segregated equilibria were in some sense stable and they were strict equilibria in the sense that you strictly preferred not to deviate. Whereas, these integrated equilibria, these were actually perhaps not stable,?a kind of weak equilibrium.?

Now, I want to bring up one other concept here, which is the idea of a "tipping point." So this is a game that was introduced by a guy called Schelling. Schelling went on to win the Nobel Prize largely for this; certainly in large part for this idea. This is a game that has a tipping point. There are really two stable equilibria, the segregation of one way and the segregation the other way, and in between there's a tipping point beyond which if you--beyond which--if you go beyond which you go to the other equilibrium.?There are two strict equilibria and if we got beyond the points of a 50/50 mix going the other way, we can whiz off to the other equilibrium.?

We already saw a game that had a tipping point when we played the investment game, where there were two equilibria, all invest and no one invest, there was a natural tipping point in that game and the tipping point was having exactly 90% of you invest, the point at which you actually would want to flip over and go to the other equilibrium. So this is a game that has a tipping point. We can push people away from the equilibrium and they'll go on coming back and they'll go on coming back and go on coming back, but if we just push them a little bit beyond a half, whoops, they'll go on off to the other equilibrium; very dramatic change. That seems like a rather important idea in, for example, sociology.?

So I've got these segregated equilibria and I've got these integrated equilibria and let's just make the other obvious remark. Which of these equilibrium is preferred by the population? Would they rather be in the integrated equilibrium, given that these are their payoffs, or the segregated equilibrium? They'd rather be in the integrated one. So here's a world in which they'd like to be in the--everybody would like to be in the integrated equilibrium. This is not a Prisoner's Dilemma. This is not a case that we've seen before but it turns out that you're likely to end up in these inefficient, less preferred by everybody, segregated equilibria.?

The other equilibrium is--actually there's two of them--is if everybody, everyone in the room chose East Town. We'd have to find a way of assigning everybody, so what we would do is we'd essentially randomize over the room and half the room would be in East Town and half the room would be in West Town. So there's this kind of silly equilibrium in a sense, in which everyone does the same thing, and the way in which people actually get allocated is not by their choice but by this detail of the original game, which was if there was overcrowding we were going to randomize people.?

So, there is actually a third equilibrium which is all--there's two of these of course--so all choose the same town and get randomized. To check that is an equilibrium, notice that if everyone else is choosing--if everyone else is playing this strategy of all choosing East Town and allowing the randomization device to place you, then you're completely happy to do that, completely happy to do the same thing. So it is in fact an equilibrium. So, this is a slightly odd equilibrium here, and there's immediately a Game Theory lesson here.?

The second lesson here is if in fact, if this randomization process was available, if in fact it was possible for everyone in the town to chose East Town and then have the local government randomize you, then if we use the law of large numbers, if there's 100,000--I guess 200,000 people in all and they're all being randomized, we're going to end up very, very close in the limit exactly at integration and everyone's going to be better off.?

So the other kind of strange thing here is having society randomize for you--ended up being better than, what you might want to call "active choice."?

One lesson might be a lesson in sociology.?In this game, segregation is what resulted, at least in the stable equilibria, and you might be tempted if you're an empirical sociologist, to go around the world and say, look I see segregation everywhere. I've gone from country to country, from society to society, and wherever I go I see segregation. You might be tempted to conclude that that's because people prefer segregation and that might be right. Nothing in this model disproves that. It might be the facts that--it might in fact be in the case that the reason you see segregation in virtually every society is because segregation is preferred. I'm not ruling that out here I'm just raising another possibility.?

What's the other possibility? The other possibility is it could be that preferences are like this, roughly speaking. People don't actually prefer segregation, but when all people act in their own interest you end up with segregation anyway. So, the fact that that we're seeing segregation in this model does not imply that there's a preference for segregation. It doesn't rule it out, of course, but you can't conclude, just because you see segregation everywhere that necessarily people want segregation. Let me just take that outside of the context of segregation, more generally. If you see a social phenomenon in society after society, after society whether they are anthropologists going across societies or a historian going through societies in historical time, and you see the same phenomenon in each of these societies which results from the choices of thousands of different people, you can't conclude from the fact that you see it in all of these societies that those people prefer it.?

All you know is that each of their individual choices add up to this social outcome that may or may not be something they prefer. In this case it's not. That was really Schelling's big idea. I don't want to write that all out but it's kind of a--it's a huge idea. It got him the Nobel Prize. So you don't want to conclude from observation straight back to preference in these strategic settings.?

What happened was they imposed randomization. They did exactly the policy that we described up here. This was essentially their policy and notice actually the policy that they adopted, the policy in which house allocation was random, was basically going to what the policy Yale had all along. So as happens in other cases in education, Harvard arrived at the Yale solution eventually. So randomization or more dramatic things like bussing are policies arrived at really because we know of the existence of these models. I'm not saying these are right or wrong.; It's not my position to say that they're right and wrong. I'm saying if you were going to argue for these policies, this might be a way in which you might argue for these policies.?

Now, I want to bring out the third lesson here, there's a Game Theory lesson here about irrelevant details; irrelevant details mattering, but I want to bring out one more Game Theory lesson here. So here we've been discussing randomization in these settings in the following form. In the game, the local governments randomized where you lived. In the bussing experiment it was randomly chosen who went to which school. I guess it was done by social security number, I don't know. In Harvard and in Yale too, there's some randomization about which college house you live in. That's one way to achieve randomization: you could have it done centrally. The central administration, this local government, the central government, can randomly assign people. But in principle, there's another way to achieve randomization. What's the other way you could achieve randomization? Both in this experiment and elsewhere.?

So rather than having centralized randomization, in principle, you could get to the same outcome by having individual randomization. So there's another possibility here, which is individual randomization. In principle, you could have everybody in the room decide that what they're going to do is throw a coin, a fair coin, each of them separately, and if it comes up heads they'll go to East Town and if it comes up tails they'll go to West Town, and if all of them do that and they all stick with it, again, by the law of large numbers we'll get pretty close to integrated towns. But it won't have been some central authority doing the randomization. it'll be each of you individually doing the randomization.?

Now, however, as soon as we introduced the idea of individual randomization we've gone a little bit beyond where we got to in the class. Because so far in the class, we've talked about strategies as the choices that are available to you. The choices available to you were go to the East Town, go to the West Town. Or, in the numbers game we played, it was choose a number. Or, in the ? β game we played, it was choose ? or β. Or deciding whether to invest or not, it was invest or don't invest, and so on and so forth. What we're seeing now is a new type of strategy. And the new type of strategy is to randomize over your existing strategies. So we're introducing here a new notion that's going to occupy us for the rest of the week, and the new notion is a randomized, or as we're going to call them, "mixed strategies."?

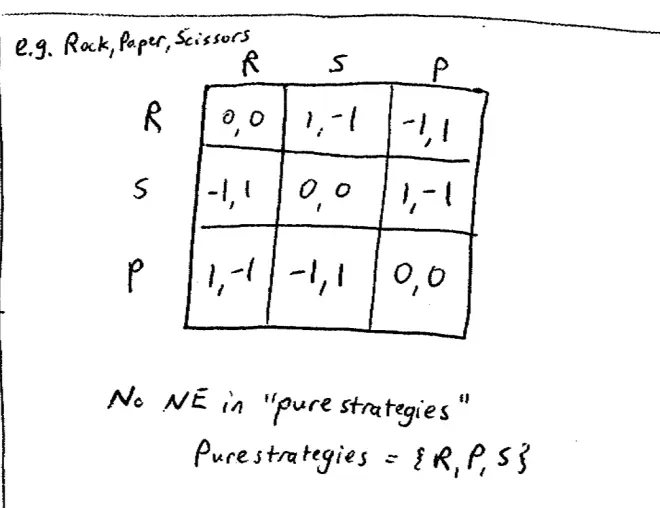
So what is--I'll be more formal next time, but what is a mixed strategy? It is a randomization over your pure strategies. The strategies that we've dealt with in the course up to now, from now on, we're going to refer to those as pure strategies, they are your choices. And we're going to expand your actual available choices to include all randomizations over those. This may seem a little weird, so to make it seem a little bit less weird, let's move immediately to an example. So, the example I want to talk about is a game that I think is familiar to a number of you, but I'll put up the payoffs and see. So the payoffs look like this; each person has--there's two players--each of them has three strategies and the payoff matrix looks as follows: (0,0) is down the lead diagonal and going around it's going to be (1,-1), (-1,1), (-1,1), (1,-1), (1,-1), (-1,1).?

This is "rock, paper, scissors." So I think, if I get this right, this better be rock, and this better be scissors actually and this better be paper. This is rock, paper, scissors.?

That's really a hint of where we're going here. That's a hint of where we're going. This is a very simple game "rock, paper, scissors," but it's pretty obvious, I hope, that pure strategies in this game are probably not enough to model this guy. So, in particular, I claim and if necessary will prove that there is no Nash Equilibrium in pure strategies, in the strategies that we've been looking at up to now. There's no Nash Equilibrium in which people choose pure strategies here. So there's no Nash Equilibrium. From now on I'm going to use the term pure strategies to mean the strategies we've been looking at so far. So by pure strategies here, the set of pure strategies is equal to the set rock, paper, and scissors; so what we've called strategies up to now in the class.?

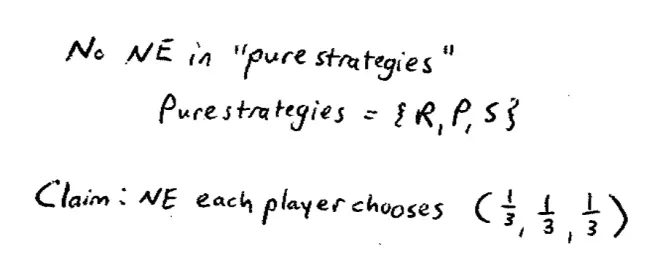
So now, can everyone see why there's not going to be a Nash Equilibrium in pure strategies? Let's just talk it through. So, if one person plays rock, the best response against rock is? Let's try that again; you all know. Best response to rock is? Paper; but if you played paper the best response to paper is? Scissors; and the best response to scissors is? Rock; so everyone knows how to play this game. So clearly, there's not going to be a pure strategies Nash Equilibrium, right? Because any attempt to look for best responses that are best responses to each other can lead to a cycle. Everyone see that? There's no hope of finding two pure strategies that are best responses to each other because of that cycle.?

So I claim as a guess that the Nash Equilibrium is each player, both players, each player chooses--and I'm going to call it 1/3, 1/3, 1/3--in other words, each player is playing the mixed strategy 1/3, 1/3, 1/3.

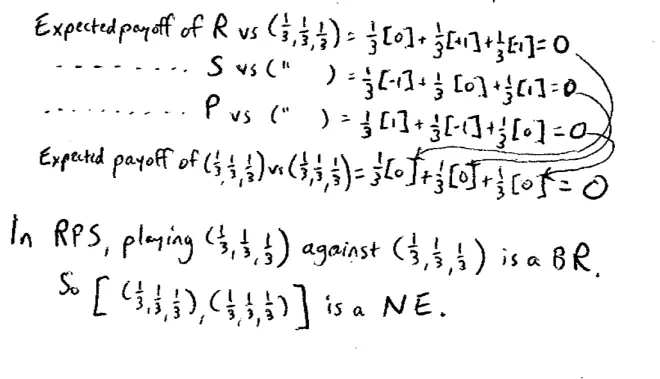
So what I'm going to do is I'm going to show you that this will in fact be a Nash Equilibrium by showing you payoffs. So what's the expected payoff--to start off, what's the expected payoff of rock against 1/3, 1/3, 1/3? So the other person's randomizing equally over rock, paper, scissors and I'm going to choose rock. What will be my payoff, my expected payoff? Well, I claim that with probability 1/3 I'll meet another rock and get 0, and with probability of 1/3 I'll meet a scissors and get -1 and with probability of 1/3 I'll meet paper--I said that wrong, let me start again. The probability 1/3 I'll meet rock and get 0, probability 1/3 I'll meet scissors and get +1, and a probability 1/3 I'll meet paper and get -1.?

So my expected payoff is 1/3 of 0, 1/3 of +1, and 1/3 of -1 for a total of 0. It's not hard to check that the same is true if I chose scissors. If I chose scissors and the other person is randomizing 1/3, 1/3, 1/3 then with probability 1/3 I will get -1, with probability 1/3 I will meet another scissors and get 0, and with probability 1/3 I'll meet paper and get 1, and once again it nets out at 0. Finally, if I played paper, and once again I'm going to meet somebody who is in fact randomizing a 1/3, 1/3, 1/3 over rock, paper, and scissors then with probability 1/3 I'll meet a rock and get 1, with probability 1/3 I'll meet scissors and get -1, and with probability 1/3 I'll meet paper and get 0.?

So each of the pure strategies here rock, paper, or scissors–actually, I did rock, scissors, and paper, each of them when they play against 1/3, 1/3, 1/3 they yield an expected payoff of 0. What about playing the mix itself? What's the expected payoff of playing--myself playing 1/3, 1/3, 1/3 if I play against somebody who's playing 1/3, 1/3, 1/3? Well, a 1/3 of the time I'm going to be playing rock, so a 1/3 of the time I'm going to be playing rock and then I'll get the expected payoff from playing rock against 1/3, 1/3, 1/3. What was the expected payoff from playing rock against 1/3, 1/3, 1/3? Zero. So, 1/3 of the time I'm going to play rock and I'm going to get this 0. And 1/3 of the time I'm going to be playing scissors, and then I'm going to get the expected payoff from scissors against 1/3, 1/3, 1/3 and what was the expected payoff of scissors against 1/3, 1/3, 1/3? Zero again. So 1/3 of the time I'll play scissors and I'll get this 0. And 1/3 of the time I'll be playing paper, in which case I'll get the expected payoff of paper against 1/3, 1/3, 1/3 which once again is 0. So my total expected payoff is 1/3 of 0, plus 1/3 of 0, plus 1/3 of 0 which, for the math phobics in the room comes, out as 0.?

So notice what we've shown here; we've shown that if I play what I claim is the equilibrium strategy 1/3, 1/3, 1/3 against 1/3, 1/3, 1/3 I get 0 and if I played any other strategy I'd still get 0.?So therefore playing 1/3, 1/3, 1/3 is indeed a best response, albeit weakly, it is indeed a best response and this is in fact a Nash Equilibrium. So what we've shown here is in "rock, paper, scissors" playing 1/3, 1/3, 1/3 against the other guy playing 1/3, 1/3, 1/3 is a best response, anything would be a best response, but in particular it's a best response. So if both people play this, one person plays a 1/3, 1/3, 1/3 and the other person plays 1/3, 1/3, 1/3, this is a Nash Equilibrium. So we're belaboring a point that we all knew already: playing 1/3, 1/3, 1/3 against--if everyone plays a 1/3, 1/3, 1/3 that is a Nash Equilibrium. It's a little harder to show but it's true, that that's the only equilibrium in the game.