ECON 159.?Game Theory

Lecture?11. Evolutionary Stability: Cooperation, Mutation, and Equilibrium

https://oyc.yale.edu/economics/econ-159/lecture-11

We're going to talk about evolution. We're going to talk about the connection between evolution and Game Theory. Why look at evolution in the context of Game Theory? There are really two reasons. The first reason is because of the influence of Game Theory on biology. It turns out that in the last few decades, there's been an enormous amount of work done in biology, in particular, looking at animal behavior and using Game Theory to analyze that animal behavior. And just to give you a loose idea about how this works, the idea is to relate strategies with genes, or at least a phenotype of those genes, and to relate payoffs to genetic fitness. So the idea is that strategies are related to genes and the payoffs in the games are related to genetic fitness. And the big idea of course, is that strategies grow if they do well. So strategies that do well in these games grow. Strategies that do less well die out.?

One thing to bear in mind from the start is that there's an important difference between Game Theory as analyzed in animal behavior and biology, and Game Theory that we've been doing so far in the class. And that is, that we're going to think of behaviors, these strategies played by animals, not as chosen by reasoning individuals but rather as being hardwired. So if strategies grow it isn't that some lion or ant has chosen that strategy. It's simply that the ant or lion who has that gene that corresponds to that strategy grows and has many children.?

So a second reason for studying this stuff is that there's been an enormous influence from biology or from evolutionary biology in particular, back on the social sciences.?This influence the other way uses evolution largely as a metaphor. And you'll find this if you're a political scientist, if you're a historian, if you're an anthropologist, if you're a sociologist. Let me give you an example from Economics, since it's perhaps closer to home. So here's an example. You might imagine some firms in the marketplace and you could think of these firms not necessarily reasoning out what is the most profitable strategy for them, or what is the most cost-reducing strategy for them. However, they may just have rules of thumb to select their strategies. However, in a competitive marketplace, survival of the fittest firms will lead to us ending up with a bunch firms who have low costs and high profits.?So here competition in the marketplace substitutes for competition in the jungle, as it were. The analog of a gene dying out is a firm going bankrupt.?

So we're going to focus on what we're going to call within species competition. So the lions are competing against the lions and the ants are competing against the ants. The way we're going to think about this is we're going to look at symmetric two-player games. So we look at very simple games, they're only going to involve two players, and they're going to be symmetric games, which means both players have the same strategies, both players have the same payoffs. The way we're going to think of is, we're going to imagine that there's a large population out there, each of whom is playing a particular strategy, and we're going to assume that what happens is, we randomly pick two people from that population and pair them up.?

So everyone in this large population will be randomly paired with someone else, they'll play the strategy that they are hardwired to play, and then we'll see what happens. So the idea here is there's a large population of, if you like animals, which are hardwired to play particular strategies, and we're going to have random matching. The idea here is when we do lots of these random matching, we're going to keep track of the average payoffs. So what we're going to focus on are the average payoffs of particular strategies when randomly matched in these games. Again, the underlying idea is that relatively successful strategies will grow and relatively unsuccessful ones will decline.

So to keep things simple today we're going to assume that there is no gene redistribution. So in principle what we're looking at is asexual reproduction, which is clearly not a good model but it will do for today.

So that's going to be our basic story, and the basic idea we're going to use is this. It's an idea due to a guy called Maynard Smith in the 70s, although obviously the big idea goes back earlier. So this is the big idea. Suppose that we imagine that there's a particular game and there's these large populations--think of yourselves as the large population--and suppose that the entire population were all playing the same strategy, call it S, so they're all hardwired to play the same strategy S. Suppose now that there's a mutation, so some small group start playing some other strategy, let's call it S'. What we want to ask is will that small mutation group, the S' strategy, will it thrive or will it die out? If it's true that, for all possible mutations, all the possible little groups of mutation of people who are playing S', they'll die out, then we'll say that the original strategy, the strategy S, is evolutionarily stable.

There's a strategy out there that everyone's playing, call it S. We're going to look at a mutation, that's S'. So a small group of people are going to start playing S'. They're going to go on being randomly matched, everyone's going to be randomly matched, and we're going to ask if the S' group does well, in which case they'll grow, or does badly, in which case they'll shrink and eventually die out. If they die out we'll say that S was evolutionarily stable, that's true for all possible mutations. Just notice when we're randomly matching them, one thing to note is since there's only a small mutation to start with, most of the time when they're randomly matched, they're going to match against somebody who's still playing S. Occasionally they're going to meet one of the other mutants, but most of the time we're going to have to worry about how the mutants do against the incumbent population.?

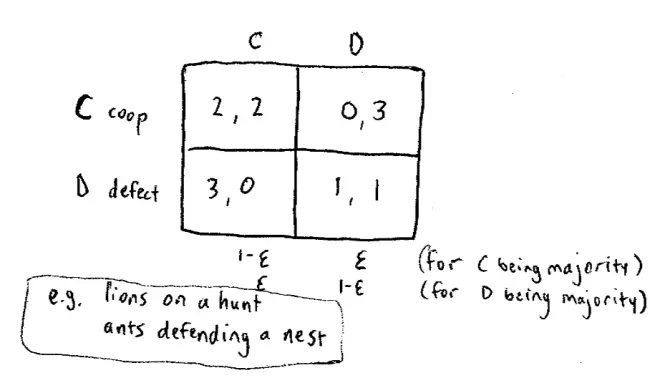
So we're going to start with a very simple example that you'll all recognize. Here's a game, it's a two-by-two game, and the payoffs are as follows, (2, 2), (0, 3), (3, 0) and (1, 1). We'll call these strategies cooperate or defect: C for cooperate, D for defect.?This is Prisoners' Dilemma. So we're going to start by imagining these animals playing Prisoner's Dilemma. And to put it into context, imagine that these are a group of lions--and again leave aside the fact that it's asexual reproduction for a second--imagine these are a group of lions. And cooperating means cooperating on the hunt, it means using a lot of energy going after--as you cooperate in a group while hunting. And defecting here would mean not working hard on the hunt and letting the other lions catch the antelope or whatever, and then just sharing in the spoils: so "free riding" basically.?

Or another example, think about ants with an ant nest, imagine this ant nest has been attacked by I don't know what, some other creature. You could imagine that cooperating is joining in, in defending the nest, at the risk of being hurt and defecting is running away. We all know in this game roughly how to analyze it. I'm not going to go over that now.

I want to ask in this model of asexual reproduction is cooperation evolutionarily stable? So the incumbent ant, the cooperative ants, they're playing, we're interested in their payoff and they're playing a population that's mixed. Almost everybody in the population is cooperative, so let's say 1 - ε of the people they're playing against (where ε is a small number, a very small number) are also cooperative, but every now and then,?they're going to come across a nasty mutant, they're going to come across Rahul. So what's their payoff going to be on average, their average payoff? So 1 - ε of the time, we can actually think of this mix here, so it's 1 - ε and ε. 1 - ε of the time they're going to meet another cooperative ant and get a payoff of 2, but ε of the time they're going to meet Rahul and get a payoff of 0. So that's their average payoff. So the mutants, there aren't many of them around, but they are also playing against the same mixed population, 1 - ε of the time they're going to be matched against a cooperative ant and ε of the time the two mutants, the two T.A.'s are going to playoff against each other.?

Let's have a look at what their payoff is. So their payoff is 1 - ε, they get a payoff of 3, that's what we saw when Rahul met Nick and the other ε of the time, Rahul meets Jake or somebody and has to make do with a payoff of 1. But if we keep track of this, what do we have? This equals 2(1--ε) and this equals 3(1--ε) + ε. Clearly, I hope this is clear, the payoff to the mutant is bigger. The payoff to the mutant is bigger which means the mutation is not going to die out. In fact it's going to grow. Mutation's not going to die out. So we can conclude that C is not evolutionarily stable. I'm going to start using ES for evolutionarily stable. So in this particular game cooperation is not ES. So we might ask what is ES in this game? Well that's not going to be hard to figure it out, since there is only one choice. I claim that D is going to be ES, but let's just prove it.?

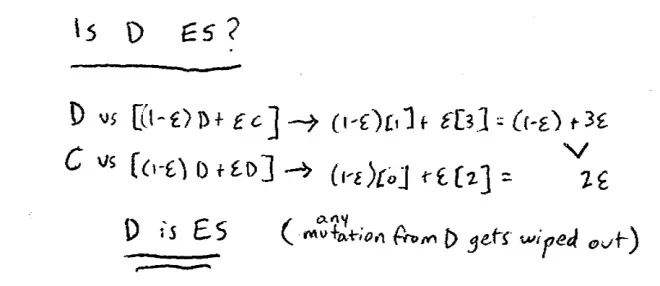
So is it going to be the case that these mutants will eventually take over the whole population and everyone will end up looking like a T.A. and being uncooperative? So they're busily asexually reproducing all the time, they get bigger and bigger, and isn't it in fact the case that once they've conquered everything that they're ES?

What's going to happen to our cooperative mutation? So most of the time you non-cooperative people are matching up against each other. We're going to figure out what your payoff is. So that the uncooperative incumbents, they're playing a population that is 1 - ε non-cooperative and ε of the time they meet Myrto. So what's their average payoffs? Let's be careful, let's switch things around up here just to make sure we can see what happened. So switching things around on our chart up here, we're now looking at the case where there's 1 - ε non-cooperators and ε cooperators. So you guys, you non-cooperative ants are most of the time meeting each other, and when you meet each other you're getting a payoff of 1. So 1 - ε of the time you're getting a payoff of 1, but ε of the time you're doing great because you're meeting Myrto, and unfortunately you're beating up on Myrto.?

How is she doing? Well she's a cooperator and 1 - ε of the time she's meeting you guys and ε of the time she meets another nice cooperative ant like Jake. So her payoff is 1 - ε of the time she gets nothing and ε of the time she does pretty well and gets 2, but it's only ε of the time. Is that right? So far, so good. So what's going to happen to this mutation? Well the incumbent population, their average payoff comes down to being 1?- ε + 3ε and Myrto's payoff, the mutant ends up being 2ε. So unfortunately, these nasty ants are thriving and Myrto gets wiped out, so she can sit down again. So what have we shown here? We've shown that defect, not cooperate, is evolutionarily stable in this game. Any mutation, there's only one possible mutation, any mutation gets wiped out. Think about these two different models here.?

The first lesson here is?nature, the outcome of evolution, nature, can suck. So again we could use a more formal term but this is an important lesson. There's a tendency for some people to think that if something arises as a consequence of evolution, if something is natural, if something is in nature, it must therefore be good in some moral way, efficient or something. What we're seeing here is in this game the consequence of nature is a horrible consequence. For those people who doubt that nature can be pretty unpleasant have a look at yesterday's science page of The New York Times, and read the piece about how the baboons basically kill the baby baboons. The biggest cause of death among baby baboons is infanticide. This is ES it turns out and they explain why in The Times. It isn't pleasant. So nature can suck, nature can be pretty inefficient.?

The assumption that's really driving this here is the assumption of asexual reproduction. sexual reproduction with gene exchange is going to make a difference.?I don't want to delve too much into the biology here, but the main why is, what matters is the survival of the gene, not survival of the individual ant or individual lion. So if you have sexual reproduction you get gene redistribution among children and cousins to a less extent, so provided the other ants in the nest are closely enough genetically related to you, and provided the lions are close enough related to you, then it may turn out to be, it may turn out that you will cooperate, and that in fact, does change the payoffs of the game. It doesn't change the payoffs for the individual lion or ant, it changes the payoffs for the gene.?

So if a strategy is strictly dominated, and of course cooperate is strictly dominated here, then it is not evolutionarily stable, at least in this simple game of just asexual reproduction. Even though I haven't proved this here, the idea is exactly the idea of this example, so let's just try and talk it through.?So?the strategy that does the domination of this strictly dominated strategy would be a successful mutation. If it enters it does well, not just against this strategy but against any mix involving itself and this strategy. So the strictly dominator strategy will invade. So we can't have strictly dominated strategies surviving in evolution.?

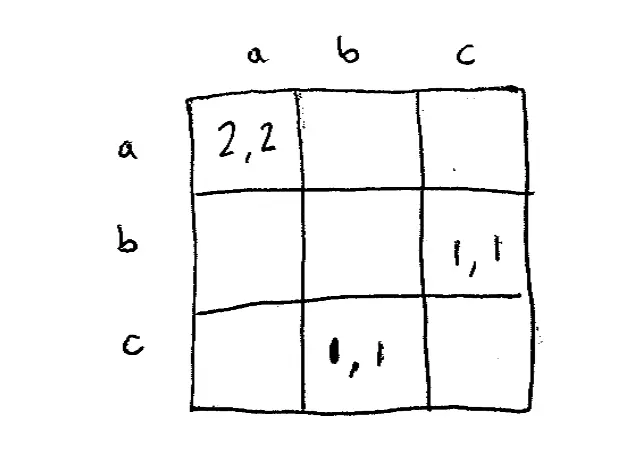
Let's do another example and we'll see if we can learn some more. So this is going to be a slightly more complicated example. Let's have a three-by-three game, so here's our three-by-three game and we'll just label the strategies A, B, C and A, B, C and once again we're going to focus on symmetric games, so this game will be symmetric: 2, 2, 0, 0, 0, 0, 0, 0, lots of zeros in this, 1, 1, 0,0, 1,1, 0,0. So this is a symmetric game. We'll look at this game a little bit, I don't want to look at all of it, I want to ask the question is strategy C evolutionarily stable??

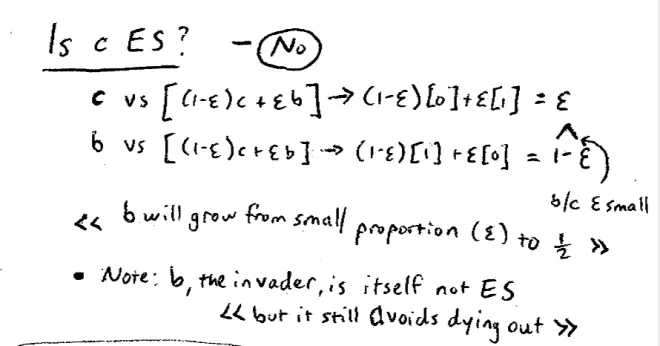
Strategy B might invade here. So suppose there's an invasion of B, so again the T.A.'s are playing B, everyone else is playing C, and let's see how these incumbent genes do. So C is playing against 1 - ε of the population who are playing C and ε who are playing B and its average payoff? Well 1 - ε of the time it'll be matched against essentially itself and get a payoff of 0, but ε of the time it will be matched against a B and get a payoff of 1.?So 1 - ε of the time it meets itself and gets nothing, ε of the time it gets lucky and it meets a T.A. and gets a payoff of 1.?

How about those B invaders, the T.A.'s in the class. So 1 - ε of the time they're going to meet C's and ε of the time they're going to meet B's and 1 - ε of the time therefore, the B is meeting a C and getting a payoff of 1, so 1 - ε of the time the T.A. is meeting one of you. And ε of the time the T.A. is meeting another T.A., playing B against B, and getting 0. So this works out as ε and this works out as 1 - ε. But notice that if ε is small, if there were just a small number of these mutations, 1 - ε is bigger than ε. Is that right? So that means that this mutation will not die out, it'll probably go on, we can actually say a bit more, it'll probably go on growing until it's roughly half the population. But, in particular, it won't die out. Since it won't die out, since the mutation doesn't die out, we can conclude that C is not evolutionarily stable.?

Now this idea, this example is a little bit more complicated than the previous example, because it turns out that the invading mutant population, the population B is itself not evolutionarily stable. Everyone see that? C wasn't evolutionarily stable because it got invaded by B. Who's going to invade B? C is going to invade B, turns out everything is exactly symmetric here. So even though we're arguing that C is not evolutionarily stable because it's invaded by B, it doesn't have to be the case that the successful mutant is itself evolutionarily stable. So in this particular example the invader, namely B, is itself not evolutionarily stable. Nevertheless, it doesn't die out but it invades the population of C's.?

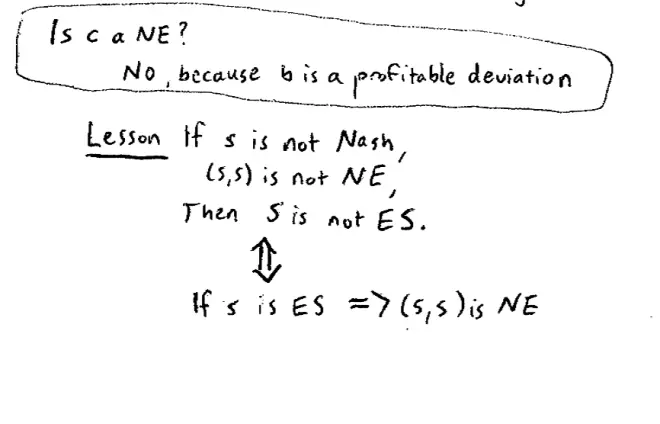
Notice that the thing that was a strictly profitable deviation was the same thing that would have invaded the population of C's in the context of our ant's nest and the context of this classroom being an ant's nest and looking at evolution. Is that right? So what have we just learned here? Well this idea turns out to be general. The idea is if a strategy S,?if a strategy S is not Nash, so in other words (S,S) is not a Nash Equilibrium, then S is not evolutionarily stable. If S is not Nash, then S is not evolutionarily stable. Now with a little bit of logic, can we flip that around and we will say, what that actually tells us is, it's equivalent to saying, if S is evolutionarily stable then (S,S) is a Nash Equilibrium, that's the equivalent way of saying that.

Let's look at the first line rather than the second line, because it's pretty easy to understand. The idea here is, if a strategy is not Nash?is there's some other strategy that would be a strictly profitable deviation and that's enough to tell us that S cannot be evolutionarily stable.?Because take that same strategy that was a strictly profitable deviation, B in this case, and that strategy can be thought of as the mutation that's going to invade the strategy we started from.?Suppose a strategy isn't, suppose strategy (S,S) is not a Nash Equilibrium. What that means is some other strategy S' say that is a strictly profitable deviation. Now think about strictly profitable deviation S' as a mutant invasion, so now Rahul is playing, is hardwired to play S'. Since it was strictly profitable it's going to be, since it was strictly profitable as a deviation, it's going to be successful as an invader. So again I haven't formally proved it, but that's exactly how the proof would run.?

So let's pause for a second and just see where we are. What we've managed to show is there's a connection here between dominance and evolutionarily stable. We've said if a strategy is not dominated it cannot be evolutionarily stable. We've also begun to show a connection between Nash Equilibrium and evolutionary stability.?We've said that if something's going to be evolutionarily stable it better be the case that it's also Nash. That raises I think a natural question which is, is the opposite true? It would be really pretty great if it were true the other way around. If I could show that if a strategy was Nash then it would necessarily also be ES. That would be pretty cool, right? This idea we've spent a lot of time developing in the class turns out to be the key idea.?

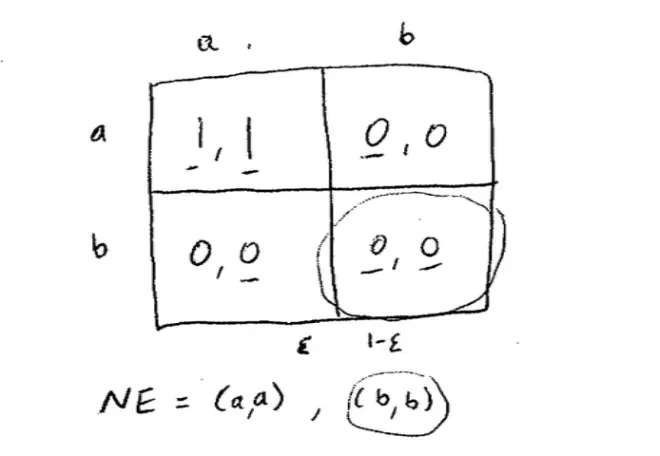
Unfortunately, life isn't quite so neat. Let's see why. So what I'm going to do is, I'm going to show you an example and what our example's going to illustrate is we can find Nash strategies that are not evolutionarily stable.?Here's a game, it's a two player, two strategy game and the payoffs are (1,1), (0, 0), (0, 0), (0, 0). This is kind of an embarrassingly simple game. What are the Nash Equilibria in this game? Well let's go through slowly. If Player row is playing A, then column's best response is to pick A and if player row is playing B, then column's best response is either to play A or B. If column is playing A, then row's best response is to choose A. If column is playing B, then row's best response is either A or B. So this is the kind of exercise that is almost second nature for you guys now. So we can conclude by looking where the Nash, where these best responses coincide, that the Nash Equilibria here are (A,A) and (B,B).?

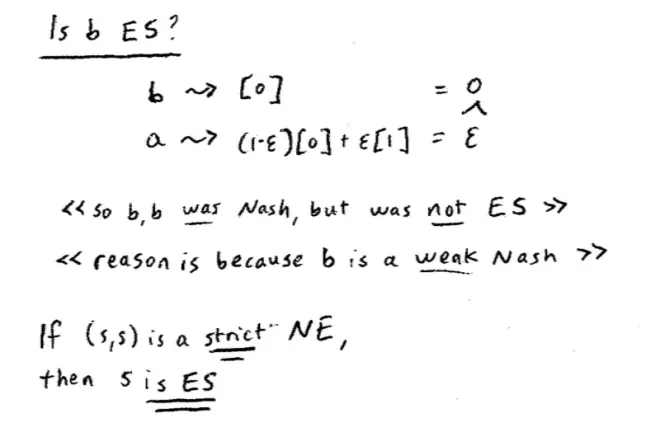
The (B,B) Nash Equilibrium, the one that's down here. Is B evolutionarily stable? Suppose the entire class were playing B. Wake up the guy in the middle and tell him he's playing B too. The whole class is playing B and suppose there's an invasion. What could the invasion be? The invasion better be an invasion of A's. What's going to be the expected payoff or the average payoff of the incumbents, of all of you in the class who are playing B? Well, without doing it too laboriously, 1 - ε of the time you're going to meet another student in which case your payoff, in which case you'll be playing B against B and your payoff will 0 and ε of the time you're going to meet a T.A. and these T.A.'s are playing A, but again, you'll get 0, so your average?payoff will be 0.?

So if you're an incumbent and you, against this mix, your payoff will be 0. And if you're an invader? So how is Rahul doing this time? Rahul's playing A. 1 - ε of the time this A is playing against B, so 1 - ε of the time he's playing against a B. So 1 - ε of the time Rahul meets a student and gets a payoff of 0. But ε of the time Rahul hits it lucky and Rahul meets another T.A., Rahul meets Jake and when he meets Jake his payoff is 1. Is that correct? So his total average payoff is ε, which is bigger than 0, so indeed, it turns out that Rahul's gene is going to grow, the B's are going to shrink. (B,B) was Nash but it's not evolutionarily stable, it can be invaded. Everyone see how that invasion worked? So the key to that invasion was when Rahul met another incumbent student he did no better than the students did against students. But on those rare occasions when Rahul met another T.A. he made hay--or not hay, it's asexual reproduction--he got a payoff of 1. Those rare occasions were enough to make Rahul grow and thrive, whereas the B's relatively speaking, shrank.?

What's true about this example is that although B is a best response against B, it only is so weakly.?It's only so weakly. If, in fact, we got rid of Nash Equilibria that relied only on weak best responses, then we wouldn't be able to produce this example. So, in particular, if we looked at Nash Equilibria, where the Nash strategy was strictly a best response, it was strictly better than playing any other pure strategy, those cases would be evolutionarily stable. Anybody remember what we call Nash Equilibria where the Nash strategy is a strict best response? We call them strict Nash, so it is in fact true, is if (S,S) is a strict Nash Equilibrium, by which I mean S is a strict best response to S, then S is a Nash equilibrium--sorry, S is evolutionarily stable.?

This is a formal definition. It comes out of biology, and in particular, it's due to a guy called Maynard Smith who wrote this in 1972. So obviously the earlier idea is due to Darwin, but this formal idea is due to Maynard Smith. So here's our formal definition. So in a symmetric two player game--so everything we've been looking at so far --, the pure strategy S--let's call it ?,--let's give it a name --, is evolutionarily stable --and again I'll use ES for that. I'm going to say in pure strategies: it's evolutionarily stable in pure strategies if, and just leave a little bit of a space here, because I'm going to need a little bit of space between these next two lines, leave a little space here.?

Let's just see why that is so. So this on the left is the payoff of ? against a population in which 1 - ε of the population like it is playing ? and ε of the population is like Rahul, because 1 - ε of the time it meets something like itself, and ε of the time it meets a T.A. Conversely, on the right hand side, we have the payoff to the mutation. The payoff to the mutation is 1 - ε of the time the T.A. meets a student and gets the payoff of S' against ?, ε of the time the T.A. meets itself and gets a payoff of S' against S', and we have this inequality we had before, that says the mutation invader has to do worse so it dies out.

So now what I'm going to do is I'm going to give you an entirely different definition.?So think of that as Definition 1, and it came from biology, it came from this paper in 1972. I think it was in Nature by Maynard Smith and co-authors. Think of this other definition, that's coming out of Economics. So Definition 2, a strategy ?--I should have had the same qualifier, in a symmetric two player game--same thing to start off with--a strategy ? is ES in pure strategies--so same as we had before if two things. Thing number one, let's call it A, if (?, ?) is a Nash Equilibrium--is a symmetric obviously--is a symmetric Nash Equilibrium of the game.?Let me just write down what it means to be a symmetric Nash Equilibrium of the game, what does that mean? That means i.e., the payoff of ? against ? must be at least as big as the payoff of S' against ? for all S'.?

We need, if this weak inequality I wrote above is actually an equality, if the payoff of ? against itself is actually equal to the payoff of S' against ?, then the payoff of ? against S' must be bigger than the payoff of S' against itself.?Let's see what it says again, it says ? is evolutionarily stable if it's a Nash Equilibrium, that's basically this and if it's only a weak Nash Equilibrium--there's a tie --, then it better beat up on the mutant. It better beat up on the mutant when it meets the mutant. I'm going to try and give you an intuition as to why this is true in a minute, but first I want to tell you why you should care about this.?

So I'm going to give you a reason?why this is an important result. It's going to turn out that when we analyze games it's very easy to check Definition 2. It's going to turn out it's very easy to check Definition 2. It's really rather a pain to check Definition 1. Why? Because you got to keep track of these ε 's and so on, but the fact that Definition 2 is equivalent to Definition 1--did I say that? That's the point. The fact that Definition 1 and 2 are equivalent--so 1 is equivalent to 2--the fact that these definitions are equivalent means we only have to check the second definition and that's easy. So when biologists are setting up experiments involving wasps or ants, or lions, or chimpanzees, provided they can check this in the game they're done, and that turns out to be easy. And we'll see that on Monday. That's the sort of instrumental reason.?

So what I'm going to do is let's fix a strategy ? and suppose (?,?) is in fact Nash. What I want to convince you of is that ? is going to be evolutionarily stable. So I claim there's two possibilities, there are two cases. The two cases are either it's the case that ? against ? does strictly better than ? against S' for all S'. So let's just be careful, since we know its Nash, we already know that the payoff of ? against itself is at least weakly better than any possible deviation, that's what it means to be Nash.?We know that ? is a best response to ?, so it must be weakly better than any possible deviation. So let's take the first case, where actually it's strictly better, and let's go back to our classroom example and suppose that--let's go back to the first definition by going back to our metaphor of the class. So you guys are all ants, and suppose that every student in the class is playing ?. You're all playing ? and suppose it's the case that in fact the payoff of ? against ? is bigger than the payoff of ? against S', and suppose that a mutation arises. So as the mutation arises, here's Rahul our mutation, and he's going to be randomly matched against one of you guys. So let's compare Rahul's payoff against this gentleman's payoff.?

Most of the time Pat is being matched against one of the rest of you, and when he's matched against one of the rest of you, he's getting the payoff ? against ?, which is U(?,?), that's what he's getting most of the time. Every now and then he's meeting a mutant. Okay fine, so every now and then he's getting a slightly different payoff, but most of the time he's getting a payoff which is U(?,?). What about Rahul? So Rahul, okay every now and then he's going to be lucky and meet another T.A., but most of the time, almost all the time he's being matched against one of you, for example he's matched against Pat. When he's matched against Pat, his payoff is U(?,S') which is lower. So Pat's payoff almost all the time is U(?,?) and Rahul's payoff almost all the time is U(?,S'). But our assumption is U(?,S') is lower, so Rahul's going to die out.?