[Electromagnetism] Cycloid Motion with EM Fields
By: Tao Steven Zheng (鄭濤)
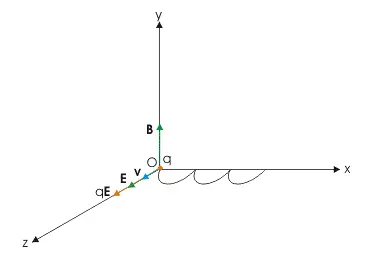
【Problem】
Consider a uniform magnetic field directed in the x-direction, and a uniform electric field directed in the z-direction. A particle with positive charge and mass
is released from the origin, and initially at rest. Determine the trajectory of the particle over time.
Hint

【Solution】
The magnetic force is calculated using the cross-product
Subsequently, the Lorentz force, , in vector form is
Divide the mass of the particle on both sides of the equation and let and
, then
To solve this system of coupled differential equations, let .
Thus,
Substitute the bottom equation into the derivative of the middle equation to obtain
The above differential equation is non-homogeneous, thus the solution is the sum of the homogeneous solution and particular solution.
(1) Homogeneous solution
The characteristic equation is , where
.
The solution is therefore
or
(2) Particular solution
Since is constant, if
, then
. Then the differential equation?
reduces to
Hence .
Consequently, the solution of the differential equation is
Since the particle is initially released at rest,
To obtain the trajectory,
Since the particle is initially released at the origin,
Replacing and
with its original quantities yields
The solution of displacement presents a cycloid trajectory!