ECON 159.?Game Theory

Lecture 01. Introduction: Five First Lessons

https://oyc.yale.edu/economics/econ-159/lecture-1

What strategic means: it's a setting where the outcomes that affect you depend on actions, not just on your own actions, but on actions of others. What I want to do is get on to where this applies. It obviously applies in Economics, but it also applies in politics, and in fact, this class will count as a Political Science class if you're a Political Science major.?Game Theory is very important in law these days. Game Theory is also used in biology and towards the middle of the semester we're actually going to see some examples of Game Theory as applied to evolution. And not surprisingly, Game Theory applies to sport.?

The main textbook is this one, Dutta's book?Strategy and Games. If you want a slightly tougher book, more rigorous book, try Joel Watson's book, Strategies. Both of those books are available at the bookstore. ?In addition, I strongly recommend people read,?Thinking Strategically.?

"Game 1, a simple grade scheme for the class. Read the following carefully. Without showing your neighbor what you are doing, put it in the box below either the letter Alpha or the letter Beta. Think of this as a grade bid. I will randomly pair your form with another form and neither you nor your pair will ever know with whom you were paired. Here's how the grades may be assigned for the class. [Well they won't be, but we can pretend.] If you put Alpha and you're paired with Beta, then you will get an A and your pair a C. If you and your pair both put Alpha, you'll both get B-. If you put Beta and you're paired with Alpha, you'll get a C and your pair an A. If you and your pair both put Beta, then you'll both get B+."?

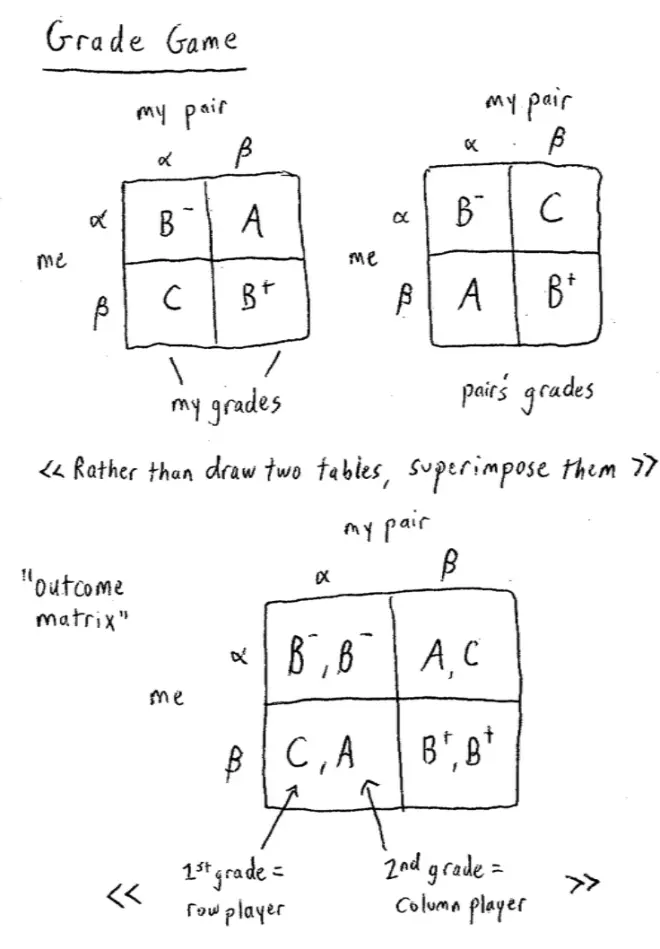
In this table, I'm going to put my grades. So my grade if we both put Alpha is B-, if we both put Beta, was B+. If I put Alpha and she put a Beta, I got an A, and if I put Beta and she put an Alpha, I got a C. Is that correct? That's more or less right? Yeah, okay while we're here, why don't we do the same for my pair? So this is my grades on the left hand table, but now let's look at what my pair will do, what my pair will get.?

So once again if you both put Alpha then my pair gets a B-. If we both put Beta, then we both get a B+; in particular, my pair gets a B+. If I put Alpha and my pair puts Beta, then she gets a C. And if I put Beta and she puts Alpha, then she gets an A. So I now have all the information that was on the sheet of paper that you just handed in.?

?Rather then drawing two different tables like this, what I'm going to do is I'm going to take the second table and super-impose it on top of the first table. Okay, so let me do that and you'll see what I mean. What I'm going to do is draw a larger table, the same basic structure: I'm choosing Alpha and Beta on the rows, my pair is choosing Alpha and Beta on the columns, but now I'm going to put both grades in. So the easy ones are on the diagonal: you both get B- if we both choose Alpha; we both get B+ if we both choose Beta. But if I choose Alpha and my pair chooses Beta, I get an A and she gets a C. And if I choose Beta and she chooses Alpha, then it's me who gets the C and it's her who gets the A.?

So notice what I did here. The first grade corresponds to the row player, me in this case, and the second grade in each box corresponds to the column player, my pair in this case. So this is a nice succinct way of recording what was in the previous two tables. This is an outcome matrix; this tells us everything that was in the game.?

If we play this game up in the business school, I think it's quite likely we're going to get a lot of Alpha's chosen.?If you played in the Divinity School, you might think that people in the Divinity School might care about other people's grades.?There might be ethical reasons--perfectly good, sensible, ethical reasons--for choosing Beta in this game. There might be other reasons as well, but that's perhaps the reason to focus on. And perhaps, the lesson I want to draw out of this is that right now this is not a game. Right now we have actions, strategies for people to take, and we know what the outcomes are, but we're missing something that will make this a game.?

We're missing objectives. We're missing payoffs. We're missing what people care about, all right. So we can't really start analyzing a game until we know what people care about, and until we know what the payoffs are. Now let's just say something now, which I'll probably forget to say in any other moment of the class, but today it's relevant.?

So we've had two different kinds of payoffs mentioned here. We had the kind of payoff where we care about our own grade, and Travis has mentioned the kind of payoff where you might care about other people's grades. And what we're going to do today is analyze this game under both those possible payoffs. To start that off, let's put up some possible payoffs for the game. And I promise we'll come back and look at some other payoffs later. We'll revisit the Divinity School later.?

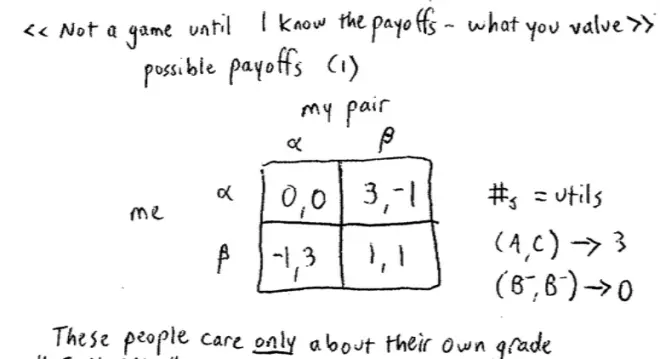
All right, so here once again is our same matrix with me and my pair, choosing actions Alpha and Beta, but this time I'm going to put numbers in here. And some of you will perhaps recognize these numbers, but that's not really relevant for now. All right, so what's the idea here? Well the first idea is that these numbers represent utiles or utilities. They represent what these people are trying to maximize, what they're to achieve, their goals.?

The idea is - just to compare this to the outcome matrix - for the person who's me here, (A,C) yields a payoff of--(A,C) is this box--so (A,C) yields a payoff of three, whereas (B-,B-) yields a payoff of 0, and so on. So what's the interpretation? It's the first interpretation: the natural interpretation that a lot of you jumped to straight away. People with these payoffs are people--who only care about their own grades. They prefer an A to a B+, they prefer a B+ to a B-, and they prefer a B- to a C.?

What do we call people who only care about their own grades? What's a good technical term for them? In England, I think we refer to these guys - whether it's technical or not - as "evil gits." These are not perhaps the most moral people in the universe. So now we can ask a different question.

It's an important idea--is this is no matter what the other person does, no matter what the pair does, she obtains a higher payoff by choosing Alpha.?If the pair chooses Alpha and she chooses Alpha, then she gets 0. If the pair chooses Alpha and she chose Beta, she gets -1. 0 is bigger than -1. If the pair chooses Beta, then if she chooses Alpha she gets 3, Beta she gets 1, and 3 is bigger than 1. So in both cases, no matter what the other person does, she receives a higher payoff from choosing Alpha, so she should choose Alpha. That's a stronger line of reasoning then the reasoning we had earlier.?

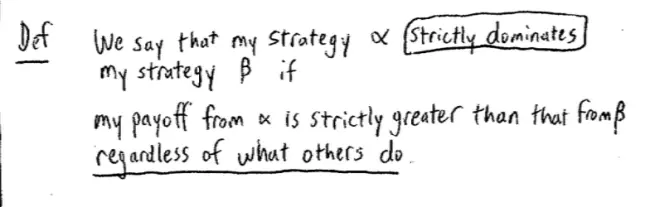
Definition:?We say that my strategy Alpha?strictly dominates?my strategy Beta, if my payoff from Alpha is strictly greater than that from Beta,?[and this is the key part of the definition], regardless of what others do.?

So Lesson One of the course is:?do not play a strictly dominated strategy. The reason I don't want to play a strictly dominated strategy is, if instead, I play the strategy that dominates it, I do Better in every case. The reason I never want to play a strictly dominated strategy is, if instead I play the strategy that dominates it, whatever anyone else does I'm doing Better than I would have done. Now that's a pretty convincing argument.?

Okay, so how about the following argument? Look at the payoff matrix again and suppose I reason as follows. Suppose I reason and say if we, me and my pair, both reason this way and choose Alpha then we'll both get 0. But if we both reasoned a different way and chose Beta, then we'll both get 1. So I should choose Beta: 1 is bigger than 0, I should choose Beta. What's wrong with that argument? My argument must be wrong because it goes against the lesson of the class and the lessons of the class are gospel right, they're not wrong ever, so what's wrong with that argument??

It involves some notion of agreeing. So certainly part of the problem here, with the reasoning I just gave you--the reasoning that said I should choose Beta, because if we both reason the same way, we both do Better that way--involves some kind of magical reasoning. It's as if I'm arguing that if I reason this way and reason myself to choosing Beta, somehow I'm going to make the rest of you reason the same way too. I'm not a character out of the X-Men, and so you can't actually see brain waves emitting from my head, and my reasoning doesn't affect your reasoning. So if I did reason that way, and chose Beta, I'm not going to affect your choice one way or the other. That's the first thing that's wrong with that reasoning. What else is wrong with that reasoning??

Even if I was that guy in the X-Men or the Matrix or whatever it was, who could reason his way into making people do things. Even if I could make everyone in the room choose Beta by the force of my brain waves, what should I then do? I should choose Alpha. If these are my payoffs I should go ahead and choose Alpha because that way I end up getting 3. So there's two things wrong with the argument. One, there's this magical reasoning aspect, my reasoning is controlling your actions. That doesn't happen in the real world. And two, even if that was the case I'd do Better to myself choose Alpha.?

So, nevertheless, there's an element of truth in what I just said. It's the fact that there's an element of truth in it that makes it seem like a good argument. The element of truth is this. It is true that by both choosing Alpha we both ended up with B-'s. We both end up with payoffs of 0, rather than payoffs of 1. It is true that by both choosing, by both following this lesson and not choosing the dominated strategy Beta, we ended up with payoffs, (0,0), that were bad.?

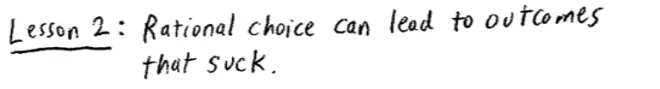
So Lesson 2, and this lesson probably wouldn't be worth stating, if it wasn't for sort of a century of thought and economics that said the opposite. So?rational choice?[in this case, people not choosing a dominated strategy; people choosing a dominant strategy]?rational choice can lead to outcomes that?- what do Americans call this?--that?"suck." If you want a more technical term for that,?it can lead to outcomes that are "inefficient," that are "Pareto inefficient," but "suck" will do for today. Rational choices by rational players, can lead to bad outcomes.?

So this is a famous example for this reason. It's a good illustration of this point. It's a famous example. This is called?Prisoner's Dilemma. In the standard story you've got these two crooks, or two accused crooks, and they're in separate cells and they're being interviewed separately--kept apart--and they're both told that if neither of them rats the other guy out, they'll go to jail for say a year. If they both rat each other out, they'll end up in jail for two years, But if you rat the other guy out and he doesn't rat you out, then you will go home free and he'll go to jail for five years. Put that all down and you pretty quickly see that, regardless whether the other guy rats you or not, you're Better off ratting him out.?

But, of course, that's not the only example. The grade game and this is not the only example. There are lots of examples of Prisoner's Dilemmas out there. Let's try and find some other ones. So I'm just guessing, having been in a few of these things over the years, that by the end of the semester, or certainly by the end of the school year, the state of the average Yale dorm room is quite disgusting. Why is it disgusting??The dorm is?disgusting because people don't tidy up. They don't clean up those bits of pizza and bits of chewed bread and cheese, but why don't they tidy up??

Well let's just work it out. What would you like to happen if you're sharing a dorm room? You'd like to have the other guy tidy up, right? The best thing for you is to have the other guy tidy up and the worst thing for you is to tidy up for the other guy. But now work it out: it's a Prisoner's Dilemma. If the other guy doesn't tidy up, you're best off not tidying up either, because the last thing you want is to be tidying up for the other guy. And if the other guy does tidy up, hey the room's clean, who cares? So either way, you're not going to tidy up and you end up with a typical Yale dorm room.?

What about an Economics example? What about firms who are competing in prices? Both firms have an incentive to undercut the other firm, driving down profits for both. The last thing you want is to have the other firm undercut you, in an attempt to push prices down. That's good for us the consumers, but bad for the firm, bad for industry profit.?

So what remedies do we see in society for Prisoner's Dilemmas? Collusion; so firms could collude. So what prevents them from colluding? One thing they could do, presumably, is they could write a contract, these firms. They could say I won't lower my prices if you don't lower your prices, and they could put this contract in with the pricy lawyer, who's taking a day off from the divorce court, and that would secure that they wouldn't lower prices on each other. Is that right? So why wouldn't that work? Why wouldn't writing a contract here work? It's against the law. It's an illegal contract. What about you with your roommates? How many of you have a written contract, stuck with a magnet on the fridge, telling you, when you're supposed to tidy up. Very few of you. Why do you manage to get some cooperation Between you and your roommates even without a written contract??

So maybe even among your roommates, maybe you don't need a contract because you can manage to achieve the same ends, by the fact that you're going to be interacting with the same person, over and over again. So we'll come back and revisit the idea that repeating an interaction may allow you to obtain cooperation, but we're not going to come back to that until after the mid-term. That's way down the road but we'll get there.?

So I promised a while ago now, that we were going to come back and look at this game under some other possible payoffs. So I wasn't under a contract but let's come back and fulfill that promise anyway. So we're going to revisit, if not the Divinity School, at least in people who have more morality than my friends up in the business school. We'll call these guys "indignant angels." So here are their payoffs and once again the basic structure of the game hasn't changed. It's still I'm choosing Alpha and Beta, my pair is choosing Alpha and Beta, and the grades are the same as they were before. But this time the payoffs are as follows.?

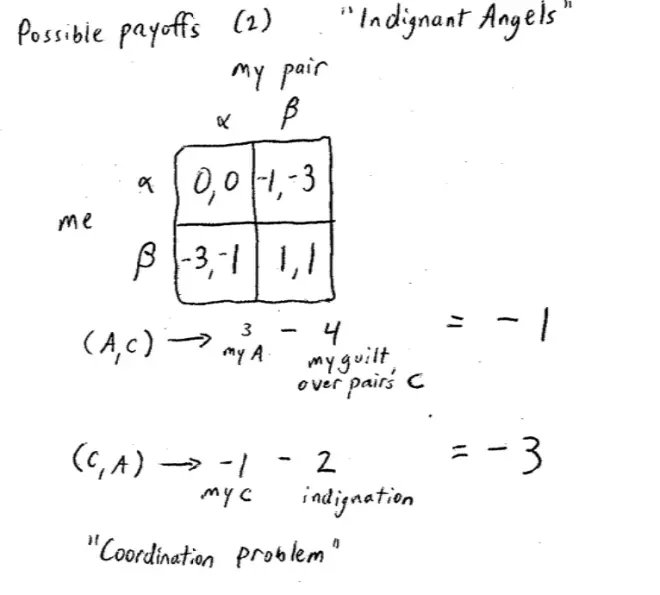
Is one of the strategies dominated in this game? No, neither strategy is dominated. Let's just check. If my pair chooses Alpha, then my choosing Alpha yields 0, Beta -3: so Alpha would be Better. But if my pair chooses Beta then Alpha yields -1, Beta yields 1: in this case Beta would be Better. So Alpha in this case is Better against Alpha, and Beta is Better against Beta, but neither dominates each other.?

So here's a game where we just change the payoffs. We have the same basic structure, the same outcomes, but we imagine people cared about different things and we end up with a very different answer. In the first game, it was kind of clear that we should choose Alpha and here it's not at all clear what we can do--what we should do. In fact, this kind of game has a name and we'll revisit it later on in the semester. This kind of game is called a "coordination problem."?

It's the lesson that payoffs matter. We change the payoffs, we change what people cared about, and we get a very different game with a very different outcome. So the basic lesson is that payoffs matter, but let me say it a different way.?

So far we've looked at this game as played by people who are evil gits, and we've looked at this game as played by people who are indignant angels. But we can do something more interesting. We can imagine playing this game on a sort of mix and match. For example, imagine that you are an evil git, but you know that the person you're playing against is an indignant angel.?

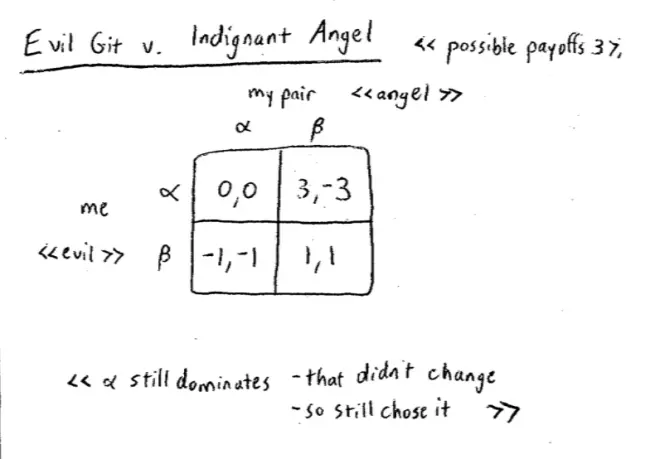
So what does this game look like? It's an evil git versus an indignant angel and we can put the payoff matrix together by combining the matrices we had before. My payoffs are going to be evil-git payoffs, so they come from the matrix up there. So if someone will just help me reading it off there. That's a 0, a 3,a -1, and a 1. My opponent or my partner's payoffs come from the indignant angel matrix. So they come from here. There's a 0, a -3, a -1, and a 1.?

The fact that I changed the other guy's payoffs didn't matter here. Alpha was dominant before--it dominated Beta before--and it still dominates Beta. If my opponent chooses Alpha and I choose Alpha, I get 0; Beta, I get -1. So Alpha would be Better. If my opponent chooses Beta and I choose Alpha, I get 3; Beta, I get 1. Once again Alpha is Better. So as before, Alpha does Better than Beta for me, regardless of what the other person does. Alpha dominates Beta. So Alpha dominates Beta here.?

Let's flip things around. Suppose now that you are an indignant angel and you're playing against, and you know this, you're playing against an evil git.?

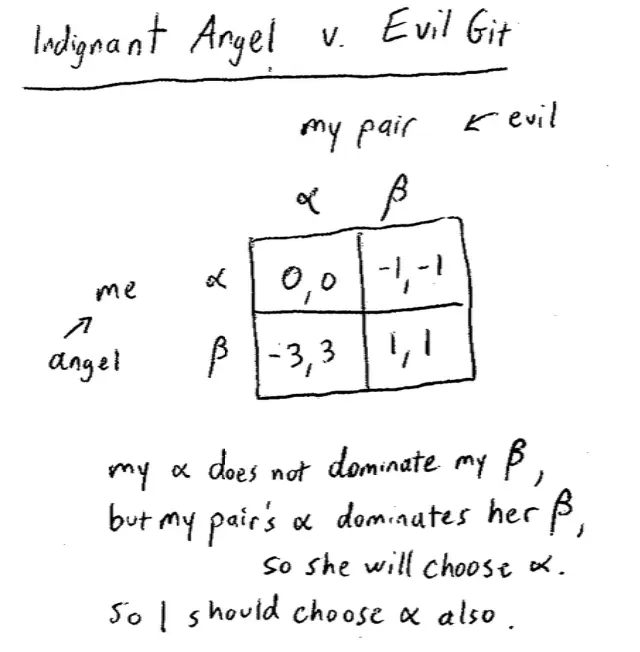
You're an indignant angel, so you have the payoffs that are still there and you're playing against an evil git, which is the payoffs we covered up but we'll reproduce them. Let's produce that matrix.

As we saw before, Alpha is Better against Alpha. Beta is Better against Beta. There's no dominance going on here. Nevertheless, at least 90% of you chose Alpha here, and that's the right answer. Why should you choose Alpha here??

I don't have a dominated strategy. My Alpha doesn't dominate my Beta. But look at my opponent. My opponent's Alpha dominates her Beta. If I choose Alpha and she chooses Alpha to get 0; Beta she gets -1. Alpha is Better. If I choose Beta, if she chooses Alpha she gets 3; Beta 1. Again Alpha is Better. For my opponent, Alpha dominates Beta. So by thinking about my opponent, by putting myself in my opponent's shoes, I realize that?she?has a dominant strategy, Alpha. She's going to choose Alpha and my best response against Alpha is to choose Alpha myself.?

So here, this time, my Alpha does not dominate Beta but my pair's choice of Alpha dominates her choice, her possible choice of Beta. So she will choose Alpha. And once I know that she's going to choose Alpha, it's clear that I should choose Alpha and get 0 rather than Beta and get -3. So I should choose Alpha also.?

So?lesson?4?of this game is: put yourself in others' shoes and try to figure out what they will do. In a sense, this is the first difficult lesson of the class. It's easy to spot when a strategy is dominant, more or less. It's pretty easy to figure out, you have to know about your own payoffs. But the hard thing in life, is getting you to come out of your own selves a bit, realizing it's "not all about you." You've got to put yourself in other people's shoes to figure out what they care about and what they're going to try and do, so you can respond well to that.?

It turns out that this game, this Prisoner's Dilemma, with the Alpha's and Beta's, or essentially the same game, has been played many, many, many times in experiments. So out there in the real world--I think we can do this here--out there in the real world when they do these experiments, they find out that roughly 70% of people choose Alpha and roughly 30% choose Beta.?

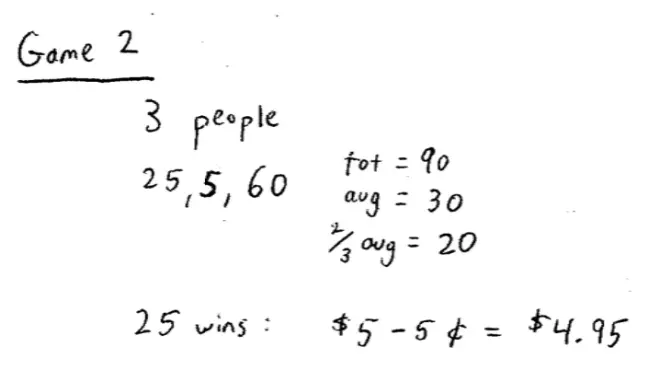
I want to play one more game today in the remaining minutes. It doesn't matter if we finish a little bit early, but I want to try to get this game at least started.?

Game 2: "pick a number." "Without showing your neighbor what you're doing, put in the box below a whole number Between 1 and a 100 [whole number Between 1 and 100--integer.] We will calculate the average number chosen in the class. The winner in this game is the person whose number is closest to two-thirds times the average in the class." [Again: the winner is the person whose number is closest to two-thirds times the average number in the class.] The winner will win $5 minus the difference in pennies Between her choice and that two-thirds of the average."?

Just to make sure you've understood this, let me do an example on the board. I've got one more board; that's good. So imagine there were three people in the class, and imagine that they chose 25, 5, and 60. So 25 plus 5 plus 60 is 90. So the average is 30. So two-thirds of the average is 20. So the average is 30 and two-thirds of the average is 20.?

The result and the corresponding rationale?will be given?in the next class.