[Geometry] Circle Segments
By: Tao Steven Zheng (鄭濤)
【Problem】
Refer to the diagram below. Prove that the total area of the red regions is equal to the total area of the blue regions.
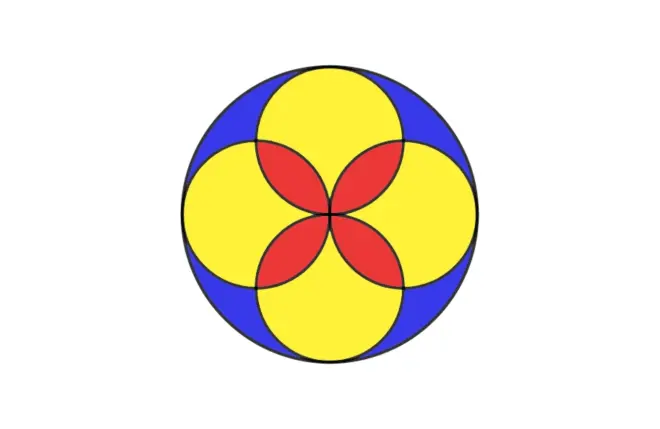

【Solution】
Due to the four-fold rotational symmetry of the diagram, this problem can be simplified by separating the circle into four quadrants and restricting the analysis to one of the quadrants.
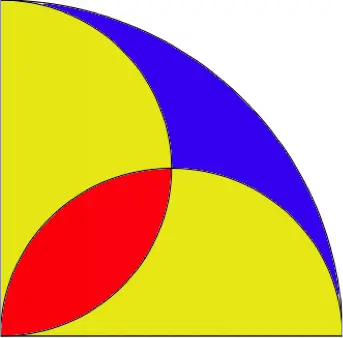
Let the radius of the quadrant be . The area of one of the yellow segments and the red segment produces a semicircle whose diameter is
. Hence, the radius of this semicircle is
. With a little calculation, it is clear that the area of the quadrant is
and the area of the semicircle is
.
This leads to the conclusion
Carrying out the algebraic calculation yields
Therefore, the area in red is equal to the area in blue.
標(biāo)簽:

