ECON 159.?Game Theory

Lecture?14. Backward Induction: Commitment, Spies, and First-mover Advantages

https://oyc.yale.edu/economics/econ-159/lecture-14

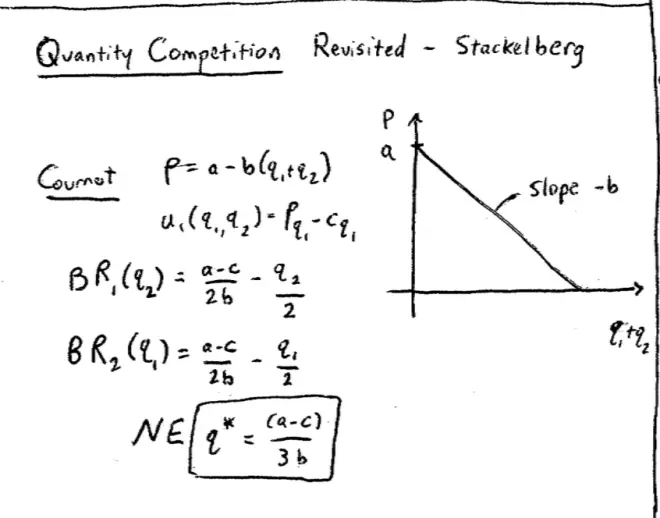
I want to go back and talk about quantity competition. So in the first half of the course we talked about price competition. We talked about quantity competition. We talked about competition with differentiated products. I want to go back and revisit essentially the Cournot Model. So this was the Cournot Model: two firms are producing, are choosing their quantities simultaneously. Firm 1 is choosing Q1 and Firm 2 is choosing Q2.?This is the demand curve. It tells us that prices depend on the total quantity being produced. So this is Q1 + Q2 and this is prices, then the demand curve is a straight line of slope b. That's what this tells us. Here's our slope –b. And we know that payoffs are just profits, which are price times quantity, revenues, minus cost times quantity, costs, we're assuming constant marginal costs.?

We figured out what the Nash Equilibrium was, and there's no prizes here: the Nash Equilibrium in Cournot was where these best responses crossed, and this is the equation for the Nash Equilibrium.?The best response for Firm 1 is a function of Q2. We're going to assume that Firm 1s moving first and the other firm--we'll assume Firm 1's going to move first--the other firm, Firm 2, is going to get observe what Firm 1 has chosen and then get to make her choice.?

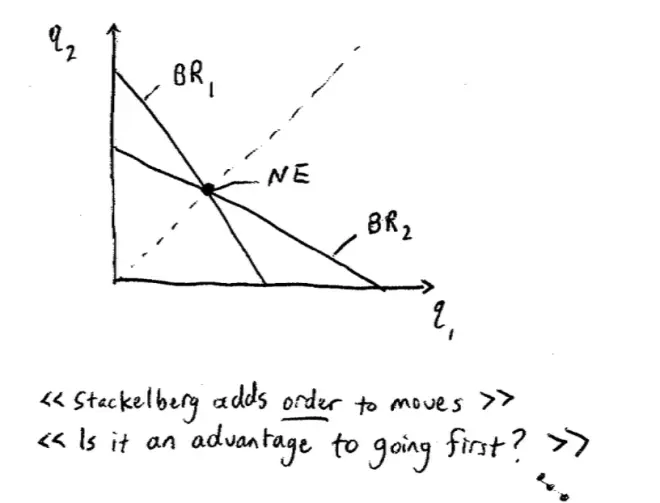
So we're going to see what difference it makes when we go from this classic simultaneous move game into a sequential move game. This model is fairly famous and I'm almost certainly spelling this wrong, but it's due to a guy called Stackelberg. So what we're looking at now is the Stackelberg Model.?A natural question to bear in mind is, assuming we're in this world of quantity competition, is it an advantage to get to move first, to set one's quantity first? Or is it an advantage to be able to wait, see what the other firm has done, and then respond? Is there an advantage in going first or is there an advantage in knowing a bit more about the other firm and being able to move second??

So this is pretty straightforward so far, but what we're able to see now, is the problem facing Firm 1, which is the interesting problem. The problem facing Firm 1 is, what quantity should Firm 1 choose knowing that this is how Firm 2 is going to respond? Before we solve this out mathematically, I just want us to think it through a little bit. So the first way I want to think this through is, is to make the following observation. From Firm 1's point of view, Firm 1 knows that any Q1 she chooses leads to a response on this line by Firm 2. That's what Firm 1 knows. So Firm 1 is effectively choosing points on this line. Let me say it again, so what's actually happening is Firm 1 is choosing Q1 and Firm 2 is responding by choosing a Q2 that puts them on this line. But in effect that means Firm 1 is choosing points on this line.?

So you could think of Firm 1's problem as, choose the joint output level on this line that maximizes Firm 1's profits. Think of Firm 1's problem as choose the combination of outputs on this line by choosing Q1 and then Q2 responds, choose the combination on this line that maximizes profits for Firm 1. So I'm belaboring this a little bit because it's a more general mathematical idea here. How many of you are in Econ?150 right now? So for those of you in Econ 150, this should be a very familiar kind of thing. This is a constrained optimization problem and you've been having constrained optimization problems rammed into you for the last month or so, so this is an example of a constrained optimization problem.?

So if Firm 2 does that, if Firm 1 chooses the Cournot quantity, then Firm 2 will also choose the Cournot quantity. So one thing that Firm 1 could do is effectively choose the old equilibrium. That's certainly something that's available to Firm 1. But Firm 1 could also do other things. Firm 1 could produce less than that or Firm 1 could do more than that. So who thinks Firm 1 should play--should choose the old equilibrium quantity? Who thinks Firm 1 should choose more than that? Who thinks Firm 1 should choose less than that? Let's just try it with the camera on you.?

Does anyone remember the jargon for this? What do we call games where the more I do of my strategy the less you do of yours? "Strategic substitutes," good. This is a game of strategic substitutes. What that means is that as Q1 goes up, Q2, the best response of Firm 2 to Q1 goes down. So what? We can look at that just by looking at the picture. Well the "so what" is, now we're in a sequential game. If Firm 1 produces more than her Cournot quantity she induces Firm 2 to produce less. That's what we just said and that's what? That's good for Firm 1. My producing more inducing you to produce less is good for me. It's going to keep prices higher in the market. Is that right??

So this suggests that Firm 1 should set Q1 bigger than Q1C?to induce Q2 to be less than Q2C. So the first thing we've learned--we'll see this in the math later--is that Firm 1 will in fact produce more than they used to under Cournot, and that will result in Firm 2 producing less than Cournot. Now we've already got a lot on the board now, we can actually solve out intuitively the problem. Do we think that Firm 1's profits, by this procedure, are the same as they were under Cournot? Are they less than they were under Cournot, or are they more than they were under Cournot??

So just let me say it again. Firm 1 is going first now. We've argued that Firm 1's going to produce more. Do we think that Firm 1's profits at the end of the day are going to be the same as they were under Cournot, higher than they were under Cournot, or lower than they were under Cournot? So let's have a poll again, let me get the camera on you guys. So who thinks their profits are going to be the same as they were under Cournot? Who thinks the profits have gone up? Who thinks the profits have gone down? We're in good shape here because indeed the profits have gone up. There's a very simple argument why the profits have to have gone up.?

The fact that Firm 1 has changed their output, and in particular, are producing more, tells you they must be able to increase their profits by this maneuver. Let's just think that through. One option that was available to Firm 1 before was to set output at the Cournot level. If Firm 1 had set output at the Cournot level, that would have led Firm 2 to set output at the Cournot level, and in that case, profits would have been exactly the same as before. The fact that Firm 1 has moved away from that must mean there are higher profits available. Say it another way, Firm 1 could have had exactly what it had before, so it must be doing at least as well as it was doing before, and the fact it has changed means it must be doing better than it was doing before.?

So indeed, Firm 1's profits have gone up. We don't even need any math to prove that: it just must be the case logically. What must have happened to Firm 2's profits? What do you think has happened to Firm 2's profits? That's not so immediately obvious. It's obvious, I think, that Firm 1's profits have gone up here because Firm 1 could have had the same old profits and has chosen something else. But it's not immediately obvious what happened to Firm 2's profits, is that right? Before we get to what's happened to Firm 2's profits let's go through an intermediate step. Let's try and ask what must have happened to total output in the market in this example--in this nice simple example.?

Now let's see if we're right. Let's go back and do the math. So I want to spend a bit of time grinding this out. So I don't claim that doing the math is fun, but I want to prove that we can do it, because otherwise everyone's going to either think that this was all kind of just blah, blah, blah, and/or people are going to be scared to do the math when it arrives on a homework assignment. So for now we're going to--more or less for the next few minutes--we're going to forget we're economists and we're going to turn into nerds. That isn't a huge transition, but we'll do it anyway.?

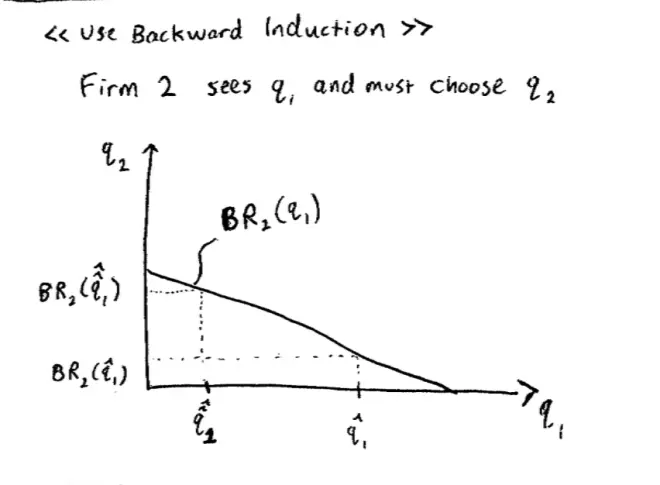
I've got the demand curve up there, so the demand the curve is still there it's P = A - B [Q1 + Q2] and I've got profits written up there, but let's put them somewhere more convenient anyway. So P = A - B [Q1 + Q2] and profit is equal to--profit for Firm i is equal to P Qi--C Qi. And what we're told to do in backward induction is what? First of all, solve things out for Firm 2 taking Firm 1 as given, and then go back and solve for Firm 1. So exactly the discussion we've just had informally, we're now going to do more formally. So backward induction tells us, solve for Firm 2 first, taking Q1 as given.?

What is that problem? It's this sort of boring math problem, it says maximize by choosing Q2 the profits of Firm 1, so that's going to be A - B Q1--B Q2. That's the price times the quantity Q2, - C Q2. So this bit here is the price. These two terms together are revenues, and this term is costs. Now I could do that, I could grind that bit out, but we already ground out that bit out three or four weeks ago right, so I'm not going to grind it out again, we know how to do that. But by the way, let's just remind ourselves what we did. We differentiated with respect to Q2. We set the thing we found, the derivative, equal to 0. That was our first order condition. And then we solved for Q2. Is that right? So when we did that, we went through the first order condition and then we solved it, we know what we actually got.?

So what we actually got was that Q2*, if you like--or Q2 let's just call it--is equal to [A - C] / 2B - Q/2. In fact, I've already given it to you up there, it's up on that top board. It's the best response for Firm 2. So again, I could do this again, but since we did it a few weeks ago I don't want to redo it. Now the more interesting part, not thrilling, but a little bit more interesting. Now let's solve for Firm 1. So what is Firm 1 doing? Firm 1 is also trying to maximize profits. Firm 1 is choosing Q1 and Firm 1--at least initially it looks like the same problem. It's A -B Q1--B Q2 Q1--C Q1, this is the same line we had before but now whereas Firm 2 was taking Q1 as given, Firm 1 knows that Q2 is given by this formula here. So what we're going to do is we're going to plug this Q2 into there.?

Now again, for those of you in 115, this isn't the only way to do it--I'm sorry 150--this isn't the only way that we could do it, we could also set up a Lagrangian equation, but for those people who don't know what that is, don't worry we're going to plug in today. So we're going to plug this in, and when we plug it in, we get a right old mess but let's do it anyway. So we're going to get max Q1, [A - B Q1--B [[A - C]/2B - Q1/2] - C] Q1. Everyone okay with that? I'm doing algebra on the board which is not fun but it's useful to do occasionally. So eventually what are we going to do? Eventually we're going to differentiate this thing, set it equal to 0, look at our first order condition and so on, just as we normally would.?

So eventually we're going to use basically 112 level calculus to solve this thing. Everyone remember how to solve a maximization problem? Yeah? But before we do that let's tidy up the algebra a bit. So this thing is--let's just tidy it up. So this is equal to max with respect to Q1--and notice I've got an A - C here and once I take this B inside the brackets I've got a--[[A -C]/2] here. So I've got an [A - C]--[[A - C]/2] so that's going to give me an [A - C]/2--and I'm really going to pray that the T.A.'s are watching me carefully and are going to catch my errors here. Okay, so I think I'm okay so far but please catch me.?

What else have I got? I've got a -B Q1 here and from in this bracket I've got a - - that's a + B Q1/2. So I have a –B Q1 + B Q1/2 so that's a –B Q1/2. So far so good and that whole thing is multiplied by Q1. Okay so far? Let's multiply out the bracket because otherwise I'll make a mistake. So this is the same as saying [A - C]/2 Q1--B Q12/2. So far so good? Now we're at the level where even my very rusty memory of calculus will get us through, so let's try and do it. So what we're going to do is we're going to differentiate this thing with respect to Q1. So differentiating with respect to Q1--let's do it up here --, we get [A -C]/2 from this term and from the –B Q12/2 we're going to get--the two's are going to cancel rather pleasantly--so we're going to get B Q1 from that term. Everyone with me so far??

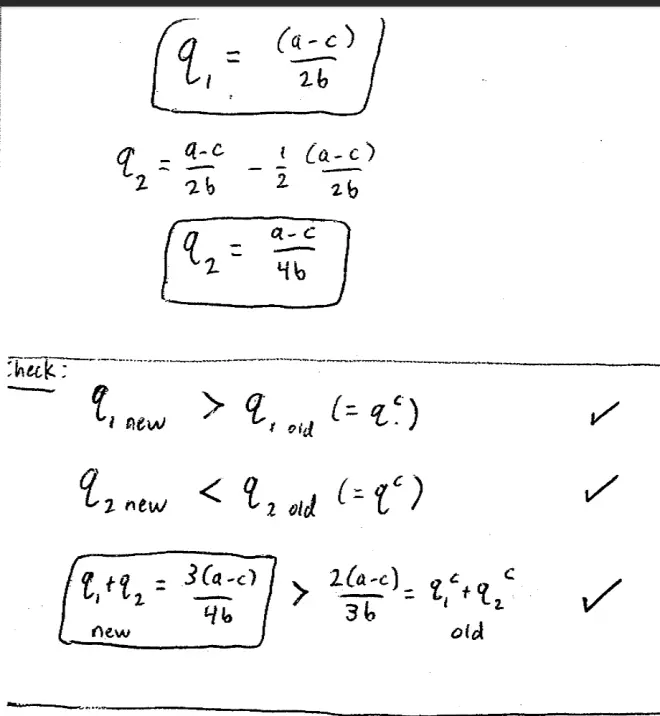
I'm going through this in sort of slow steps, I agree it's not exciting but I want to make sure I don't make a mistake. So to turn this into a first order condition what must be true about this derivative? At the maximum, what must be true about this derivative? Should be equal to 0, good, and we should just check the second order condition. How do I check the second order condition? I differentiate again and check it's negative, but if I differentiate again I'm just going to get -B. So -B is certainly negative all right, so second order condition is okay. So let's solve it out. Solving this for Q1, I get Q1 = [A - C]/2B. So we're leading in sheer boredom, it has to be done occasionally, Q1 = [A - C]/2B. We're not done yet. Now we want to go back and solve out algebraically for Q2.?

I know what Q1 is now, Q1 is [A - C]/2B. How do I find Q2? Somebody? Shout it out, how do I find Q2? I've got to plug it in. I'm going to go back and plug this Q1 back into this expression here, so I plug it back in, I'll get Q2 = [A - C]/2B - 1/2 [A - C]/2B for a total of [A - C]/4B. Is that right? That's what I have in my notes. This looks good. So I'm now done. I've now found the equilibrium. I've found that in this leader-follower game, this Stackelberg version of quantity competition, Q1 is given by [A - C]/2B and Q2 is given by [A - C]/4B.?

So our claim was that we think the new Q1 is bigger than the old Cournot quantity. So now Firm 1 is producing [A - C]/2B, previously it was producing [A - C]/3B, so that is indeed bigger, that's good news. So this is indeed bigger than Q Cournot. And our claim was that Firm 2 will produce less than the old Cournot quantity. So Firm 2 used to produce [A - C]/3B and now it's producing [A - C]/4B, and that is indeed less than the old Cournot quantity. So far so good. What about total output? How do I solve for total output? Add the two outputs together, that's not too hard. So Q1 + Q2 = [A - C]/2B + [A - C]/4B which is in fact 3[A--C]/4B. Is that right? So it's going to be 3[A--C]/4B. So I've just--actually, for the first time today, I skipped a step, but is that okay? A half plus a quarter is three-quarters. So total output is 3[A - C]/4B.?

So we started off with a question, who would you rather be Firm 1 or Firm 2, and we know the answer now. Who would you rather be Firm 1 or Firm 2? Firm 1 because Firm 1's profits went up and Firm 2's profits went down. Let's just talk about this a little bit--about what's going on here. So previously Firm 1 and 2 were just setting quantities simultaneously. We know now there's an advantage in going first. So suppose we change the game from the simultaneous move game, to a game in which Firm 1 and Firm 2 can make announcements. They can announce how much they're going to produce. So Firm 1 comes in one day and says, I'm going to produce this much and Firm 2 comes in and can see Firm 1's announcement.?

So I've changed it into a sequential game, Firm 1 has announced how much it's going to produce, Firm 2 is going to go afterwards. Is that really a sequential game? Is that going to make a difference? Why is that, I claim that's not really enough. Let me say it again. We start from the simultaneous move again. If we just change it by simply allowing Firm 1 to announce what they're going to produce--don't actually produce it but just announce what they're going to produce --, you might think that's a sequential move game and you might think that Firm 1 now has an advantage. But I'm claiming that's not enough really to give Firm 1 an advantage. Why? Why is that not enough? Let's try and get some ideas here. Let me come around to this side. So Patrick why is that not enough?

And they're moving into this new market and the market is a town. Both of them are going to issue newspapers in this market that currently doesn't have any newspapers, and Murdoch simply says I'm going to produce lots of newspapers. There's no reason for NBC to believe that. So moving first here, it isn't enough to say you're going to move first, it isn't enough even to make a decision that's reversible. Even if Q1 moved but that decision could be undone that isn't enough. What we need, and Patrick gave us the key word, what we need is commitment: a word that came up last week. So for moving first to help you here there really has to be commitment. Let's just get some of this down. There really needs to be commitment for this to work.?

So going back to the example of Murdoch and his competitor, Murdoch actually has to build the plant. There actually has to be a factory that he's built in, and that factory can't just be sold for scrap. So what creates the commitment, in the case when you've built the plant is what? Because having built it, it's a sunk cost, it's there. So sunk costs can help here. It can help making you committed. Once that money's gone, you can't get it back, so you're really committed to that scale. Does everyone know what I mean by sunk costs, by the way? So here's a case where a strategic move, entering first and sinking some investments can help you in the marketplace. Let's also look at this another way.?

Let's again go back to the simultaneous move game that we had before, where Murdoch and his competitor, the NBC parent corporation, are in fact, going to move simultaneously. Both of them are in the business of discussing how big a newspaper plant to put in this new town which hasn't got a newspaper yet, somewhere in Alabama or something. Suppose that there are two boardrooms, both of which are avidly just trying to discuss how big a newspaper plant to build. So suppose that one of the boardrooms, these four people in this row, this is the NBC parent company boardroom and they're trying to decide how big a plant to build. And over on the other side of the room is our Murdoch group which is in fact--let's take the row parallel--so these guys over there are Murdoch, are News International Group.?

So Murdoch has a spy in the NBC boardroom. So Murdoch has a little advantage here, information wise. Why? Because the NBC boardroom doesn't know what's going on in the Murdoch boardroom, but the Murdoch boardroom is going to know what's going on in the NBC boardroom. But to make the problem more interesting, suppose that somebody tells NBCs parent company, that in fact, there is a spy in their boardroom. So these guys know they have a spy, they don't know who it is.?

Usman is suggesting is maybe you don't feed Murdoch a fake plan, you feed Murdoch the true plan. Effectively, what's going to happen now is if NBC decided to build a large plant, this information will be fed back to Murdoch, and Murdoch is now in the position of being the second mover. When Murdoch moves, he or she knows what NBC is doing, and NBC knows that Murdoch is going to choose a best response to that. So it's as if NBC has been put in the position of Firm 1 and Murdoch has been put in the position of Firm 2. Even with the correct plan--so the correct thing to do here for NBC is not necessarily to mislead Murdoch, but just go ahead and build a big plant. Have that information be fed to Murdoch and let Murdoch respond to it.?

So notice here's a slightly paradoxical thing. You might think that having a spy in the camp of the other team, you might think having a spy would help you. But here having a spy--or having more information if you like--can actually end up hurting you. Everyone see that? Paradoxically, Murdoch ends up losing by the fact that he was able to predict what NBC was going to do. Now there's a key to this of course. It was crucial to the argument. What was crucial to the argument? It was crucial to the argument that NBC knew that Murdoch had a spy. The key here is that the other side, the other players, knew you had or were going to have more information. So what's the bigger idea here??

There are two bigger ideas. Bigger idea number one is, games being simultaneous or sequential is not really about timing per se, it's about information. It's about who knows what, and who knows that who's going to know what. In a situation where Firm 1, our boardroom over here, knows that Murdoch is going to have this information before Murdoch moves, that's actually a sequential game. The timing is somewhat irrelevant. So that's the first observation, and the second observation is already on the board. What we have learned is sometimes in strategic settings--sometimes not always--more information can hurt you. Sometimes more information can hurt. We have to be careful here because that's not always true but sometimes it's true. And the reason that's true is--the reason is it can lead other players to take actions, in this case, to create a large plant, that hurt you.?

Now, if you put Monday's lecture together with today's lecture, we've seen something--two very similar things arose. On Monday's lecture having fewer options, burning your boats, ended up helping you or having lower payoffs by putting collateral down ended up helping you. And that might seem like a paradox but it isn't really a paradox because what happened was provided the other side knows you have fewer options, they know you've burnt your boats, or they know you'll suffer if you default on the loan, they know you've posted collateral, it will lead them to take behavior that helps you. In the case of the loan, it led to the lender giving you a bigger loan. In the case of the Saxon Army, you at least hope at least that the Saxon Army's running away. Today, we see that more information can hurt you, and once again, it isn't really a paradox, it's the same kind of argument.?

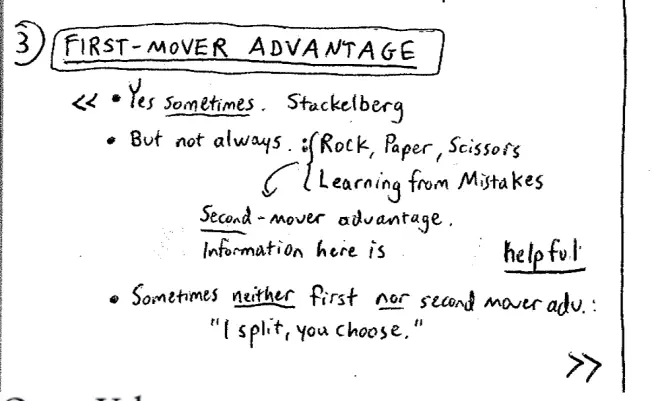
In quantity competition it's good to set your quantity, to be committed and that will lead the other side to producing smaller quantity which helps you. So sure, there are situations, there are games in which you want to move first, but there are also games in which you'd rather move second. Let me give you an example. This is an example we've seen in this class before- rock, paper, scissors. If anybody is going to read those books and believe them, so if anyone's going to read 'How to Discover Your Inner Bill Gates' and base their life on it, and therefore, think there's a first move advantage, I want to play rock, paper, scissors with that person. Everyone happy that you'd rather go second in rock, paper, scissors? Do I need to prove that or is that obvious? Okay good.?

Let me just expand a little bit more, into a more real world setting. There are plenty of settings in the real world where the advantage of moving second isn't because as in, rock, paper, scissors you just get to crush the other guy, it's simply that you learn from their mistakes. So, for example, in the game of buying new equipment for the office or home it's great to move second. The other guy goes out and samples some new piece of equipment, I wait to see if it works, and then buy it if it does. Or if I'm setting up a Firm in a new expanding market, let's say in a new part of the former Soviet Union, I'm quite happy to let some other firms go in there first and then watch what they did and try and learn from their mistakes. If I'm setting a new curriculum for a university, I'm quite happy to let other universities, Duke and Cornell and so on, move first and then I can go in as Yale, see what they did, and for sure they'll have made mistakes and I'll learn from them.?

So there's plenty of obvious situations where moving second helps you, for the obvious reason that information is often very useful. We argued here, information can hurt you, but there's plenty of other perfectly natural situations where information is to your advantage. So there are games with first mover advantages, but there also games with second mover advantages. And let me give you one example of a game that neither has a first mover advantage or a second mover advantage, just to convince you that can happen as well. So when you were a child you probably occasionally had to divide a cake and/or candy bar with your sibling. Anyone been in this situation? There was some candy bar or cake and you had to divide this thing between you and your brother and/or sister, is that right? There's a way in which, there's a typical way in which we divide things among siblings in that setting. There's a game we play to divide it. What's the game we play anyone? I'll cut and you choose, or vice versa, right. So I'll cut and you choose neither has first a mover advantage or a second mover advantage--assuming you can cut accurately, neither has a first mover advantage or a second mover advantage, which is precisely why it's a good?way to divide the candy bar.?