By: Tao Steven Zheng (鄭濤)

【Problem】

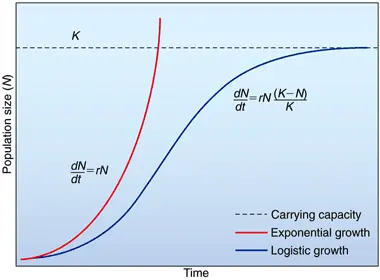
The logistic growth model is a population model that incorporates Malthusian-like growth in the early stage and in-species competition for resources at the later stage. This model includes a growth rate and carrying capacity . The differential equation of this growth model is

with the initial condition .

Part 1: What are the steady-state solutions?
Part 2: Solve the differential equation with the aforementioned initial condition.

【Solution】

Part 1

Steady-state solutions occur when for all time . For the logistic growth model,

Solving for shows that the steady-state solutions occur at and .

Part 2

Rewrite the differential equation as .

Integrate both sides

by partial fractions using the fact

Consequently,

Let , then

Solve the initial-value problem:

Consequently, the solution of the logistic growth model is