ECON 159.?Game Theory

Lecture?04. Best Responses in Soccer and Business Partnerships

https://oyc.yale.edu/economics/econ-159/lecture-4

So last time we introduced a new idea and the new idea was that of best response. The idea was to think of a strategy that is the best you can do, given your belief about what the other people are doing.?And you could think of this ─ you could think of this belief as the belief that rationalizes that choice.?

What we're going to do is we're going to look at some numbers that are approximately the probabilities of scoring when you kick the penalty kick in different directions. So the rough numbers for this are as follows.?There are three ways, the attacker could kick the ball. He could kick the ball to the left, the middle, or the right. The goalie can dive to the left or the right. In principle the goalie could stay in the middle. We'll come back and talk about that later. So this is the guy who is shooting, he's called the shooter and this is the goalie.?

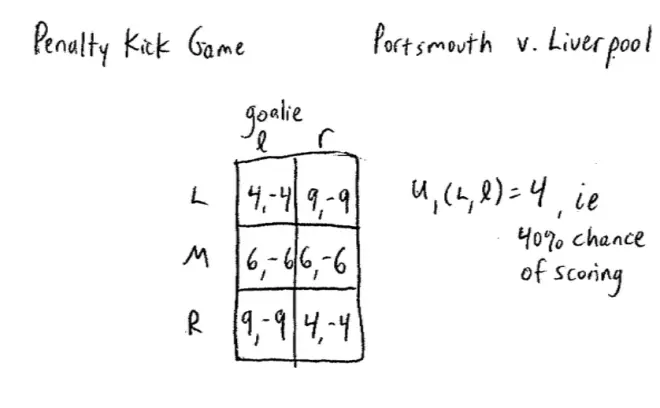
So you'll notice that I'm just going to put in numbers here and then the negative of the number and the numbers are roughly like this: (4,-4). So the numbers are (4, -4), (9, -9), (6, -6), (6, -6), (9, -9) and (4, -4). And the idea here is that the number 4 represents 40% chance of scoring if you shoot the ball to the left of the goal and the goal keeper dives to the left. So the payoff here is something like u1(left) if the goal keeper dives to the left is equal to 4, by which I mean there's a 40% chance of scoring.?

The payoff for the shooter is his probability of scoring and the payoff for the goal keeper is just the negative of that. As I said before, for now we'll ignore the possibility that the goal keeper could stay put. So how should we start analyzing this important game? Well we start with?the idea of dominant strategies. Neither of these?players here have a dominated strategy.

We're going to assume these are the correct numbers and we're going to see if that even split is really a good idea or not. What I suggest we do is we do what we did last time and we start to draw a picture to figure out what my expected payoff is, depending on what I believe the goalie is going to do.?

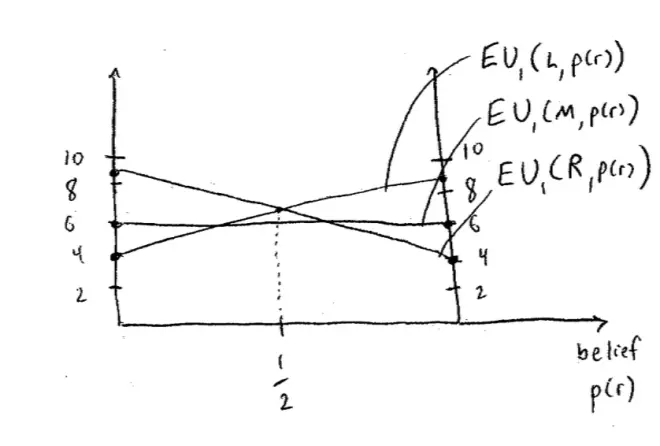
So on the horizontal axis is my belief, and my belief is essentially the probability that the goalie dives to the right. Now as I did last time, let me put in two axes to make the picture a little easier to draw. So this is 0 and this is 1.?

So it starts with a possibility of shooting to the left. So I shoot to the left and the goalie dives to the left, my payoff is?4. If I shoot to the left and there's no probability of the goalie diving to the right, which means that they dive to the left, then my payoff is 4, meaning I score 40% of the time. If I shoot to the left and the goalie dived to the right, then I score 90% of the time, so my payoff is .9. By the way why is it 90% of the time and not 100% of the time? I could miss; okay, I could miss. That happens rather often it turns out, well 10% of the time.?

So we know this is going to be a straight line in between, so let's put this line in.?It's the expected payoff to Player I of shooting to the left as it depends on the probability that the goal keeper dives to the right.?

So middle: so if I shoot to the middle and the goal keeper dives to the left, then my payoff is .6, is 6, or I score .6 of the time, and if I shoot to the middle and the goalie dives to the right I still score 60% of the time, so once again it's a straight line in between. So this line represents the expected payoff of shooting to the middle as a function of the probability that the goal keeper dives to the right.?

Let's look at the?expected payoffs, if I shoot to the right. So if I shoot to the right and the goalie dives to the left, then I score with probability .9, or my payoff is 9. Conversely, if I shoot to the right and he or she dives to the right, then I score 40% of the time, so here's my payoff .4. And here's my?line representing my expected payoff as the shooter, from shooting to the right, as a function of the probability that the goalie dives to the right.?

So the thing that I hope jumps out at you from this picture is (no great guesses about figuring out this is a ?), so if the probability that the goalie's going to jump to the right is less than a ?, then the best you can do?is shoot to the right. So the goalie is?going to dive to the right with the probability less than a ?, you should shoot to the right.?

Conversely, if you think the goalie's going to shoot to the right with probability more than a ?, then the best you can do is shooting to the left, or if you think the goalie's going to dive to the right with the probability more than a ?, the best you can do, your best response is to shoot to the left.?

And?there is no belief you could possibly hold given these numbers in this game that could ever rationalize shooting the ball to the middle.?To say it another way,?middle is not a best response to?any belief I can hold about the goal keeper, to any belief.?

There's a more general lesson here, and the more general lesson is, of course: do not choose a strategy that is never a best response to anything you could believe. That doesn't just mean beliefs of the form, the goalie's going to dive left or the goalie's going to dive right. It means all probabilities in between. So we're allowing you to, for example, to hold the belief that it's equally likely that the goalie dives left or dives right.?

But if there's no belief that could possibly justify it, don't do it. And underlining what arises in this game, notice that in this game we're able to eliminate one of the strategies, in this case the strategy of shooting to the middle, even though nothing was dominated. So when we looked at domination and deleted dominated strategies, we got nowhere here. Here, at least, we got somewhere, we got rid of the idea of shooting to the middle.?

So one thing that's clearly missing here is I'm ignoring that in fact right footed players find it easier to shoot to their left, which is actually the goalie's right. So right footed players find it easier to shoot to the left as facing, to shoot across the goal. It's a little easier to hit the ball hard to the opposite side from the side which is your foot and that's the same principle in baseball. It's a little bit easier to pull the ball hard then it is to hit the ball to the opposite field.?

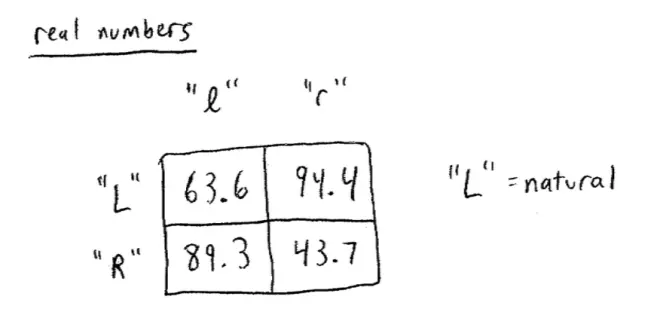
Let me put up some real numbers and we'll see about how much the correspondence to what we've got here. So the idea here is shooting to the left if you're right footed is the natural direction, so left here means the natural direction. Of course, if you're left footed it goes the other way, but they've corrected for that.?

It turns out that the probabilities of scoring here are as follows, 63.6, 94.4, 89.3, and 43.7. So you can see that whoever it was who said, you're slightly better off, you score with slightly higher probabilities when you kick to your natural side is exactly right. The thing is still not dominated and we could still have done exactly the same analysis, and actually you can see I'm not very far off in the numbers I made up, but things are not perfectly symmetric.?

Another decision you face is do you just try and kick this ball as hard as you can or do you try and place it.?That's probably as important a decision as placing it, as deciding which direction to hit, and it turns out to matter. So, for example,?if you're the kind of person who can kick the ball fairly hard but not very accurately, then it actually might change these numbers. If you can kick the ball very hard, but not very accurately, then if you try and shoot to the left or right, you're slightly more likely to miss. On the other hand, as you shoot to the middle, since you're kicking the ball hard, you're slightly more likely to score.?

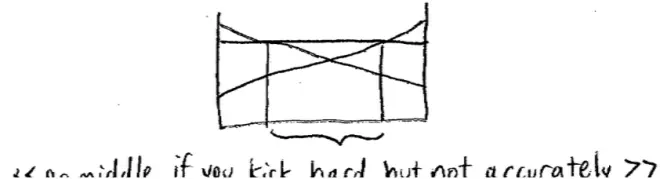
So if you're the kind of person who can kick the ball hard but not accurately, then it's going to lower the probabilities of scoring as you kick towards the right because you might miss, and it's going to lower the probability of scoring as you hit towards the left because you're likely to miss, and it might actually raise the probability of your scoring as you hit towards the middle, because you hit the ball so hard it's really pretty hard for the goal keeper to stop it. Here it goes in the middle, and if you look carefully there, I didn't really make it clear enough, you can see, suddenly a strategy that looked crazy shooting to the middle, that suddenly started to seem okay.?

It turns out, if you look at those dotted lines, there's an area in the middle,?you actually might be just fine shooting to the middle. So in reality, we need to take into account a little bit more, and in particular, we need to take into account the abilities of players to hit the ball accurately and/or hard.?

So I want to be formal about these things I've been mentioning informally. And in particular, I want to be formal about the definition of best response. I'm going to put down two different definitions of best response, one of which corresponds to best response to somebody else playing a particular strategy like left and right, and the other is just going to correspond to the more general idea of a best response to a belief.?

So Player i's strategy, ?i?(there's going to be a hat to single it out) is a best response (always abbreviated BR), to the strategy S- i?of the other players if ─ and here's our real excuse to use our notation ─ if the payoff from Player i from choosing ?i?against S- i?is weakly bigger than her payoff from choosing some other strategy, Si', against S- i?and this better hold for all Si' available to Player?i.?

So strategy ?i?is a best response to the strategy S- i?of the other players if my payoff from choosing ?i?against S- i, is weakly bigger than that from choosing Si' against S- i, and this better hold for all possible other strategies i could choose. There's another way of writing that, that's kind of useful, or equivalently, ?i?solves the following. It maximizes my payoff against S- i. So you're all used to, I'm hoping everyone is used to seeing the term max.?

Let's generalize this definition a little bit, since we want it to allow for more general beliefs. So just rewriting, Player i's strategy, same thing, ?i?is a best response. But now best response to the belief P about the other player's choices, if ─ and it is going to look remarkably similar except now I'm going to have expectation ─ if the expected payoff to Player i from choosing ?i, given that she holds this belief P, is bigger than her expected payoff from choosing any other strategy, given she holds this belief P; and this better hold for all Si' that she could choose. So very similar idea, but the only thing is, I'm slightly abusing notation here by saying that my payoff depends on my strategy and a belief, but what I really mean is my expected payoff. This is the expectation given this belief.?

Once again, we can write it the other way, or ?i?solves max when I choose Si, to maximize my expected payoff this time from choosing Si?against S-i. What do I mean by expected payoff? Just in our example, so just to make clear what that expectation means, so for example, the expected payoff to Player i in the game above from choosing left given she holds the belief P is equal to the probability that the goal keeper dived to the left, times Player i's payoff from choosing left against left, plus the probability that the goal keeper dived to the right, times Player i's expected payoff from choosing left against right. Okay, so expectation with respect to P just means exactly what you expect it to mean.?

There are two individuals who are going to supply an input to a joint project. So that could be a firm, it could be a law firm, for example, and they're going to share equally in the profits.?So they're going to share equally in the profits of this firm, or this joint project, but you're going to supply efforts individually.?

So the players are going to be the two agents and they own this firm let's call it. They own this firm jointly and they split the profits, so they share 50% of the profits each. So it's a profit-sharing partnership. Each agent is going to choose her effort level to put into this firm. So, it could be that you're deciding, as a lawyer, how many hours you're going to spend on the job. So for most of you these decisions will be a question of whether you spend 20 hours a day at the firm or 21 hours a day at the firm, something like that. For most of you on your homework assignments, I'm hoping it's a little less than that, but not much less than that.?

So the strategy choices, we're not going to do it in hours, let's just normalize and regard these choices as living in 0 to 4, and you can choose any number of hours between 0 and 4. Just to mention as we go past it, a novelty here. Every game we've seen in the class so far has had a discrete number of strategies. Even the game, when you chose numbers, you chose numbers 1, 2, 3, 4, 5, up to a 100, there were 100 strategies. Here there's a continuum of strategies. You could choose any real number in the interval [0, 4].?

When you're working on your homework assignments, if your product, the thing you hand in was just S1?+ S2.?You might think there's no point working in a study group at all. If the product is just the sum or multiple of a sum of the inputs, there wouldn't be much of a point working in a team at all. It's the fact you're getting this extra benefit from working with someone else that makes it worth while working as a team to start with. So we can think of this term has to do with complementarity, or synergy, a very unpopular word these days but still: synergy. So we're going to assume that when you work together there are some synergies. Some of you are good at some parts of the homework, some of them are good at other parts of the homework. And so in this law firm, one of these guys is an expert on intellectual property and the other one on fraud or something.?

So the payoffs: the payoff for Player I is going to depend, of course, on her choice and on the choice of her partner, and it's going to equal a ?--because they're splitting the profits--so a ? of the profits. So a ? of 4 times S1?plus S2?plus B S1?S2. She gets half of those profits but it also costs her S1?squared. So S1?squared is her effort costs, it's her input costs. This is the effort cost. Similarly, Player II's payoff is the same thing. This term is the same except we're going to subtract off Player II's efforts squared: S2squared.?

Now?we're going to analyze this using the idea of best response. So, in particular, I want to figure out what is Player I's best response to each possible choice of Player II? What is Player I's best response for each possible choice S2?of Player II? How should I go about doing that? How should I do that? So here what we did before was we drew these graphs with probabilities, with beliefs of Player I and the problem here is, previously we had a nice simple graph to draw because there were just two strategies for Player II.?

So here's Player I's payoff as a function of what Player II chooses and what Player I chooses, so we have that already. We have Player I's payoff as a function of the two efforts and now I want to find out what is Player I's best efforts given a particular choice of S2.?So we're going to use calculus. We want to take a derivative of this thing. We're asking the question, what is the maximum, choosing S1, of this profit. Can I multiply the ? by the 4 just to save myself some time? So the profit is 2 S1?plus S2?plus B S1?S2?minus S1?squared. We're asking the question, taking S2?as given, what S1?maximizes this expression and as the gentleman at the back said, I'm going to differentiate and then I'm going to set the thing equal to 0.?

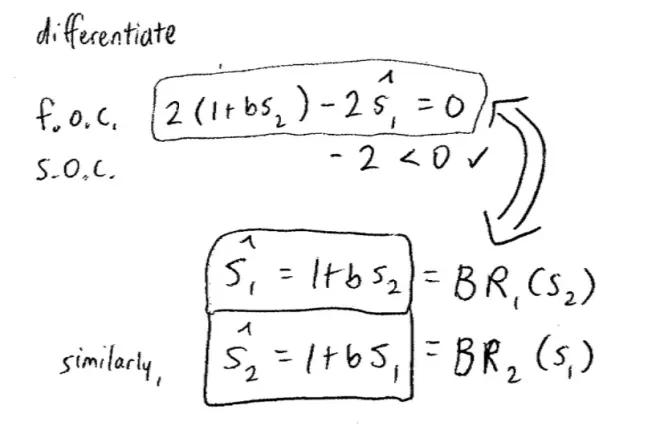
So I differentiated this object, this is my first derivative and I set it equal to 0. Now in a second I'm going to work with that, but I want to make sure I'm going to find a maximum and not a minimum, so how do I make sure I'm finding a maximum and not a minimum? I take a look at the second derivative, which is the second order condition. So I'm going to differentiate this object again with respect to S1,. Pretend the hat isn't there a second. And none of this has an S1?in it, so that all goes away. And I'm going to get minus 2, which came from here: minus 2 and that is in fact negative, which is what I wanted to know.?

To find a maximum I want the second derivative to be negative. So here it is, I've got my first order condition. It tells me that the best response to S2?is the ?1?that solves this equation, that solves this first order condition. We can just rewrite that, if I divide through by 2 and rearrange, it's going to tell me that ?1, or if you like, ?1?is equal to 1 plus B S2. So this thing is equal to Player I's best response given S2. So similarly, I would find that ?2?equals 1 plus B S1?and this is the best response of Player II, as it depends on Player I's choice of effort S1.?

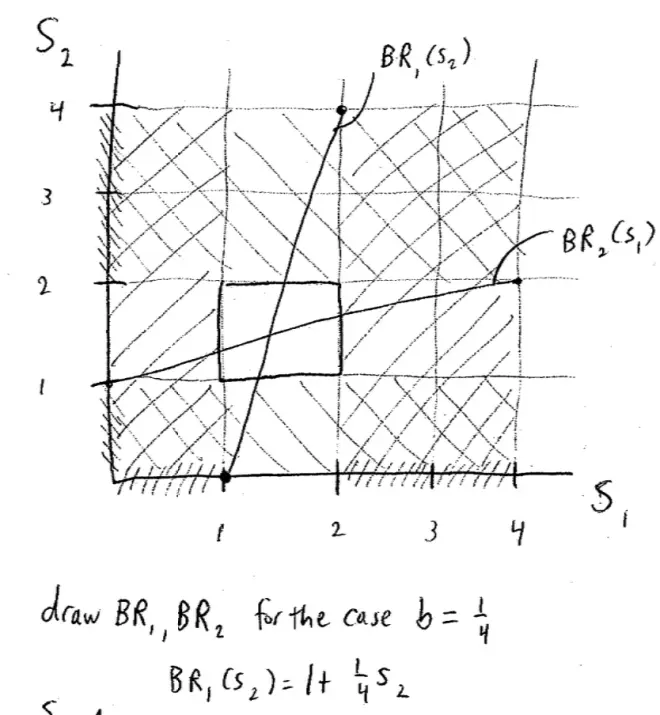
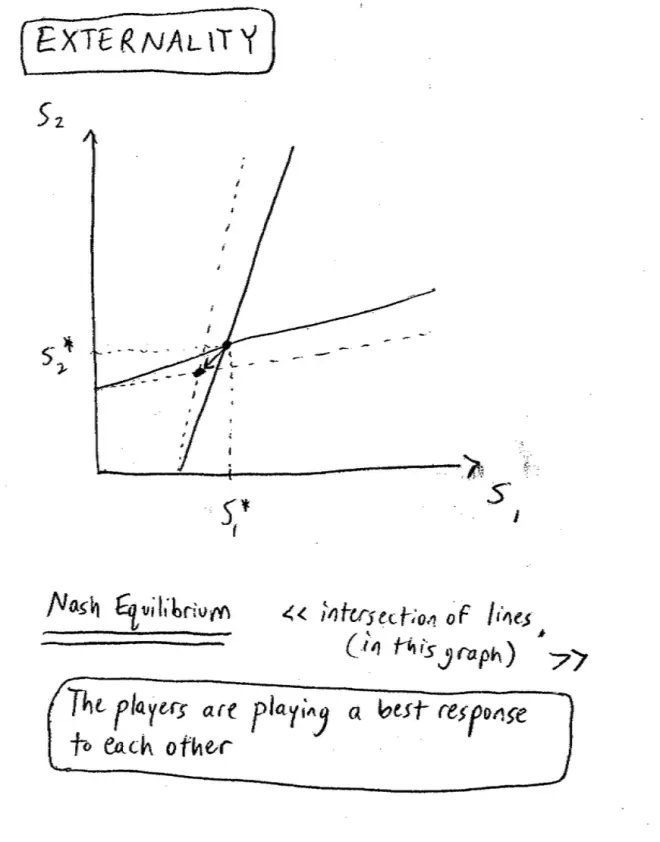
Let's draw a picture that has S1?on the horizontal axis and S2?on the vertical axis. And there are different choices here 1, 2, 3, and 4 for Player I, and here's the 45o line. If I'm careful I should get this right 1, 2, 3, and 4 are the possible choices for Player I. Now before I draw it I better decide what B is going to be.?

The way we read this graph, is you give me an S2, I read across to the pink line and drop down, and that tells me the best response for Player I. Now we can do the same for Player?II, we can draw Player II's best response as it depends on the choices of Player I, but rather than go through any math, I already know what that line's going to look like. So if I drew the equivalent line for Player II, which is Player II's best response for each choice of Player I, we're simply flipping the identities of the players, which means we'll be reflecting everything in that 45o line. So it'll go from 1 here to 2 here, and it'll look like this. So this the best response for Player II for every possible choice of Player I, and just to make sure we understand it, what this blue line tells me is you give me an S1, an effort level of Player I.

If Player II chooses 0 then Player I's best response is 1, and that's as low as he ever goes. So these strategies down here less than 1 are never a best response for Player I. If Player II chooses 4, then the synergy leads Player I to raise his best response all the way up to 2, but these strategies up here above 2 are never a best response for Player I. So the strategies below 1 and above 2 are never a best response for Player I. Similarly, for Player II, the lowest Player I could ever do, is choose 0, in which case Player II would want to choose 1, so the strategies below 1 are never a best response for Player II. And the strategies above 2 were never a best response for Player II.?

Let's get rid of all these strategies that are never a best response. So I claim if you look carefully there's a little box in here that's still alive. I've deleted all the strategies that were best--that are never best responses for Player I and all the strategies that are never best responses for Player II, and what I've got left is that little box.?

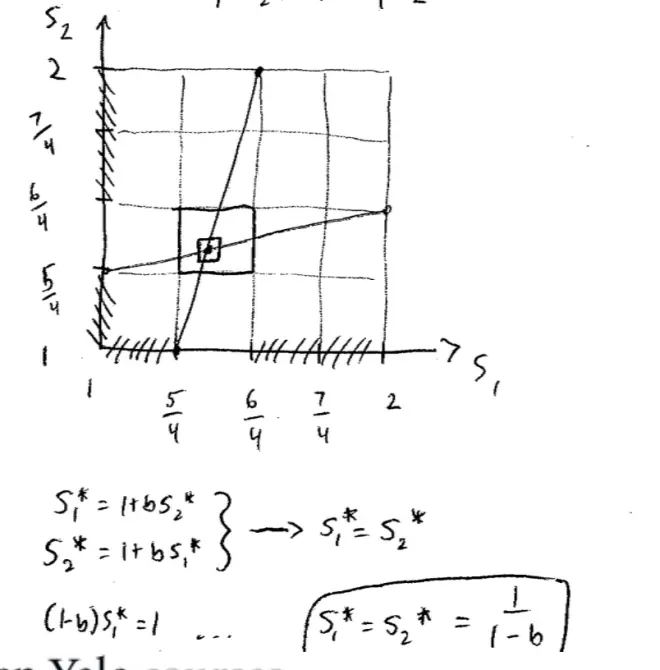
But I can't see that little box, so what I'm going to do is I'm going to redraw that little box. So let's redraw it. So it goes from 1 to 2 this time. I'm just going to blow up that box. So this now is 1, 1 and up here is 2, 2 and let's put in numbers of quarters, so this will be, what will it be? It'll be 5/4, 6/4 and 7/4, and over here it'll be 5/4, and 6/4, and 7/4. And let's just draw how those, that pink and blue line look in that box. This is just a picture of that little box, so it's going to turn out it goes from--the pink line goes from here to here and the blue line goes from here to here. We can work it out at home and check it carefully, but this isn't that incorrect.?

That's the picture we just had, except I've changed the numbers a bit. Once I deleted all the strategies that were never a best response and just focused on that little box of strategies that survived, the picture looked exactly the same as it did before, albeit it blown up and the numbers changed.?

So some of the strategies that we didn't throw away were best responses to things, but the things they were best responses to have now been thrown away. This should be something familiar from when we were deleting dominated strategies.?

Well, for example, for Player I we know now that Player II is never going to choose any strategy below 1, and so the lowest Player II will ever choose is 1, and it turns out that the lowest Player II would ever do in response to anything is 1 and above, never leads Player I to choose a strategy less than 5/4. The highest Player II ever chooses is 2, and the highest response that Player I ever makes to any strategy 2 or less is 6/4, so all these things bigger than 6/4 can go. Let's be careful here. These strategies I'm about to delete, it isn't that they're never best responses, they were best responses to things, but the things they were best responses to, are things that are never going to be played, so they're irrelevant.?

So we're throwing away all of the strategies less than 5/4 for Player I and bigger than 6/4 for Player I, (which is 1? for Player I) and similarly for Player II. And if I did this--and again, don't scribble too much in your notes--but if we just make it clear what's going on here, I'm actually going to delete these strategies since they're never going to be played--I end up with a little box again.?

So everyone see what I did? I started with a game. I found out what Player I's best response was for every possible choice of Player II, and I found out what Player II's best response was for every possible strategy of Player I. I threw away all strategies that were never a best response, then I looked at the strategies that were left. I said those strategies that were a best response to things that have now been thrown away, but not best response otherwise, I can throw those away too. And when I threw those away, I was left once again with a little box, and I could do it again, and again, and again.?

If I keep on constructing these boxes within boxes, so the next box would be a little box in here.?I'm going to converge in on that intersection.?

So what we're going to converge in on to, is the S1*, let's call it in this case, is equal to 1 plus B S2* and that S2* is equal to 1 plus B S1*. Actually, we can do it a little better than that, since we know the game is symmetric, we know that S1* is actually equal to S2*. So taking advantage of the fact that we know S1?is equal to S2?(because we're lying on the 45o line), I can simplify things by making S1* equal to S2*. So now I've got--actually, that looks like three equations, it's really just two equations, because one of them implies the other. And I can solve them, and if I solve them out I'm going to get something like (let me just be careful) I'm going to get something like: 1 minus B S1* is equal to 1, or S1* equals S2* is equal to 1 over (1--B).?

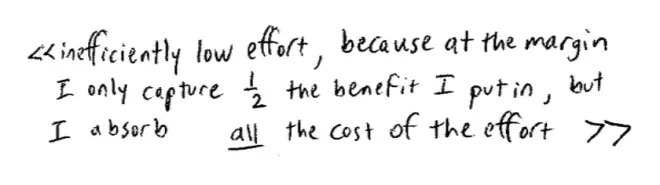
The problem here isn't really about the amount of work. It isn't even, by the way, about the synergy. You might think it's because of this synergy that they don't take into account correctly. That isn't the problem here. It turns out even without the synergy this problem would be there. The problem is that at the margin, I, a worker in this firm, be it a law partnership or a homework solving group, I put in, I bear the cost, at the margin, I bear the full cost at the margin for any extra unit of effort I put in, but I only reap half the benefits. At the margin, I'm reaping, I'm bearing the cost for the extra unit of effort I contribute, but I'm only reaping half of the induced profits of the firm, because of profit sharing.?

That leads all of us to put in too little effort. What's the general term that captures all such situations in Economics? It's an "externality." It's an externality. There's an externality here. When I'm figuring out how much effort to contribute to this firm I don't take into account that other half of profits that goes to you. So this isn't to do with the synergy.?

While we've got this on the board, let's just think a little bit more. What would happen if we changed the degree of the synergy? If we lowered B,?the?line is actually going to get steeper and?moving towards the vertical, and the blue line is going to move towards the horizontal, and notice that the amount of effort that we generate, goes down dramatically, goes down in this direction. So if we lower the synergy here, not only do I contribute less effort, but you know I contribute less effort, and therefore you contribute less effort and so on. So we get this scissors effect of looking at it this way. We could draw other lessons from this, but let me try and move on a little bit.?

We decided in this game to solve it by looking at best responses, deleting things that were never a best response, looking again, deleting things that were never a best response, and so on and so forth, and luckily, in this particular game, things converged and they converged to the points where the pink and the blue line crossed. What do we call that point? What do we call the point where the pink and the blue line cross? That's an important idea for this class. That's going to turn out to be what's called a?Nash Equilibrium.?

If Player I is choosing this strategy and Player II is choosing her corresponding strategy here, neither player has an incentive to deviate. Another way of saying it is: neither player wants to move away. So if Player I chooses S1*, Player II will want to choose S2* since that's her best response. If Player II is playing S2*, Player I will want to play S1* since that's his best response. Neither has any incentive to move away. So more succinctly, Player I and Player II, at this point where the lines cross, Player I and Player II are playing a best response to each other. The players are playing a best response to each other. So clearly in this game, it's where the lines cross.?

Let's go back to the game we played with the numbers. Everyone had to choose a number and the winner was going to the person who was closest to 2/3 of the average. (By the way, the winner's never picked up their winnings for that, so they still can.) So in that game, what's the Nash Equilibrium in that game? Everyone choosing 1. If everybody chose a 1, the average in the class would be 1, 2/3 of that would be 2/3 and you can't go down below 1, so everyone's best response would be to choose 1.?

Say it again: if everyone chose 1, then everyone's best response would be to choose 1, so that would be a Nash Equilibrium. Did people play Nash Equilibrium when we played that game? No, they didn't. Not initially at any rate, but notice as we played the game repeatedly, what happens? As we played the game repeatedly, we noticed that play seemed to converge down towards 1.?In this game, when we analyzed the game repeatedly, it seemed like our analysis converged towards the equilibrium. Now that's not always going to happen but it's kind of a nice feature about Nash Equilibrium. Sometimes play tends to converge there.