[Geometry] Two Runners
By: Tao Steven Zheng (鄭濤)
【Problem】
?Jiuzhang Suanshu (Gougu 14)
Suppose there are two persons standing at the same place. Person A walks at the rate of 7, and person B walks at the rate of 3. B walks to the east. A walks 10 bu south, then walks diagonally northeast until meeting B. Question: How far did each person walk?
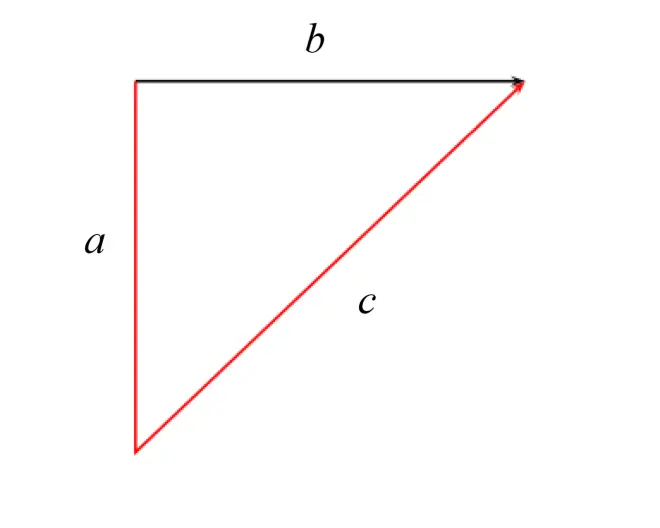

【Solution】
Here is the solution found in the ''Jiuzhang Suanshu'':
Answer: Person B travels 10.5 bu; person A travels 14.5 bu diagonally.
Method: Let 7 be multiplied by itself, and 3 also be multiplied by itself, add them and halve the result. Let this be the rate of A walking diagonally. Subtract the diagonal walking rate from the square of 7. The remainder is the rate of A walking south. The rate of B walking east is 3 times 7. Set the 10 bu walked south and multiply this by the rate of A walking diagonally. Again set the 10 bu walked south by the rate of B walking east. Let each of these be individual dividends. Divide each dividend by the rate of A walking south to obtain both distances.
This problem is an application of Pythagorean triples. First compute the rates of the height, base, and hypotenuse. According to the method the height, base, hypotenuse are called the southern ratio, the eastern ratio, and the diagonal ratio respectively.
Let , and
,
Given that person A traveled 10 bu due south before travelling diagonally, the distance traveled by person B is
The diagonal distance travelled by person A is
Person A travelled 24.5 bu (10 bu south, 14.5 bu diagonal), and person B travelled 10.5 bu (east).
[Geometry] Two Runners的評論 (共 條)
 你需要登录后才可以评论。
你需要登录后才可以评论。
