By: Tao Steven Zheng (鄭濤)

【Problem】

The napkin ring problem dates back to Edo Japan. Seki Kowa (1642 - 1708), the leading Japanese mathematician at the time was the first person to have solved this problem using a form of integral calculus called ''Enri''. Seki Kowa called the shape an “arc ring”.

The animation below shows a central cross-section of a sphere of radius? through which a centrally placed cylinder of radius has been drilled out and the material removed. The remaining shape is called a napkin ring. Determine the volume of the napkin ring.

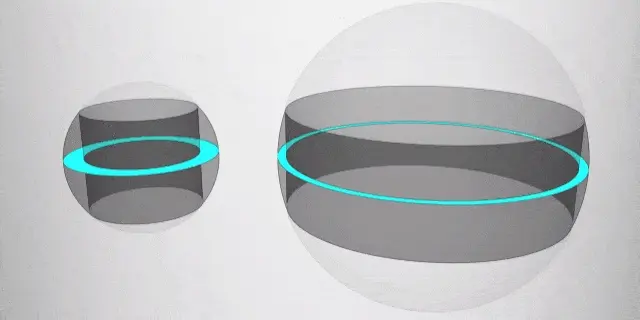
【Solution】

Consider the diagram of the cross-section of the napkin ring below. Let the radius of the sphere be . Let radius of the cylindrical hole be , and half the height of the cylindrical hole be .

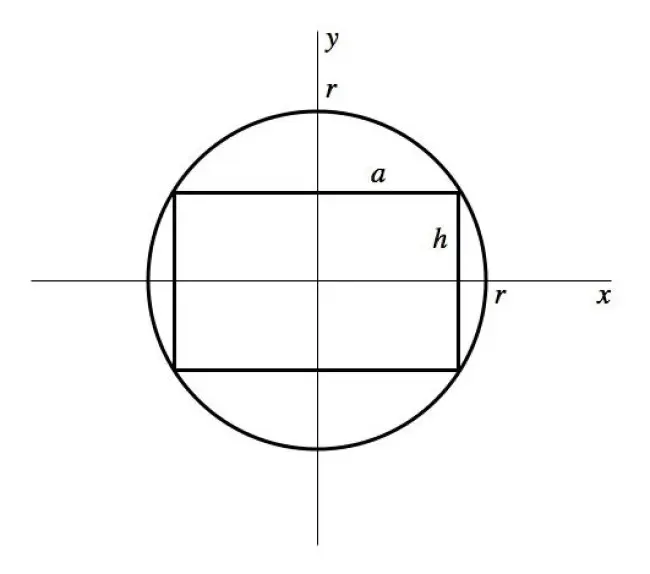
To compute the volume of the napkin ring, observe that its volume is equal to:

The volume of the sphere and the cylinder are well known:

Note that

Use integration to compute the volume of a spherical cap.

Hence, the volume of the napkin ring is:

Since , we get

The volume of the napkin ring expressed in terms of the height of the cylindrical hole, where , is:

Note that this volume is independent of the radius of the sphere, who would have guessed! This looks unbelievable at first because it means that if you core out any sphere of any size so that the remaining rings have the same height, those rings will also have the same volume!