ECON 159.?Game Theory

Lecture?09. Mixed Strategies in Theory and Tennis

https://oyc.yale.edu/economics/econ-159/lecture-9

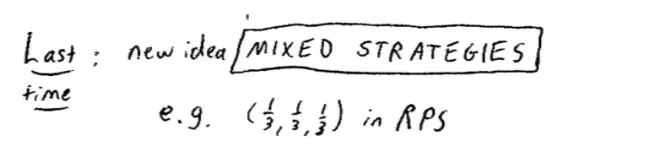
So last time we saw this, we saw an example of a mixed strategy which was to play 1/3, 1/3, 1/3 in our rock, paper, scissors game. Today, we're going to be formal, we're going to define mixed strategies and we're going to talk about them, and it's going to take a while. So let's start with a formal definition: a mixed strategy,?Pi?is a randomization over i's pure strategies. So in particular, we're going to use the notation Pi?(si) to be the probability that Player i plays si given that he's mixing using Pi. So Pi(si) is the probability that Pi?assigns to the pure strategy si.?

In principle Pi(si) could be zero. Just because I'm playing a mixed strategy, it doesn't mean I have to involve all of my strategies. I could be playing a mixed strategy on two of my strategies and leave the other one with zero probability.?The probability assigned by my mixed strategy to a particular si could be one. It could be that I assign all of the probability to a particular strategy. That's a "pure strategy."

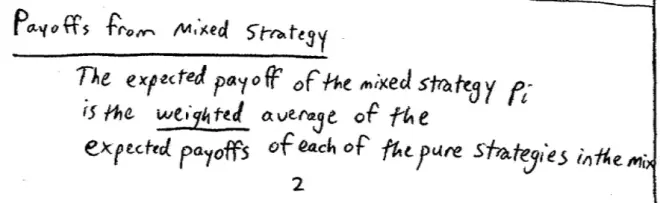
So the expected payoff of the mixed strategy Pi is?a weighted average or a weighted mixture of the expected payoffs of each of the pure strategies in the mix.?The way in which we figure out the expected payoff of a mixed strategy is, we take the appropriately weighted average of the expected payoffs I would get from the pure strategies over which I'm mixing.?

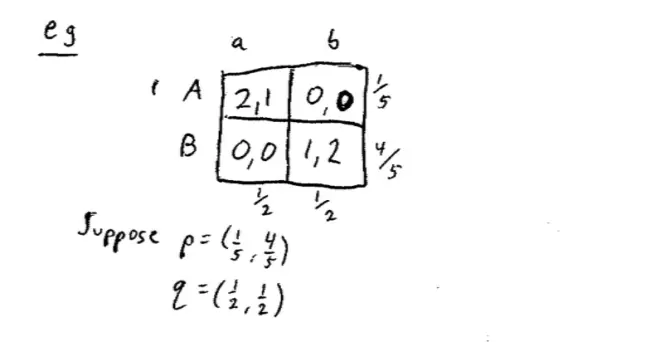
Here is the game Battle of the Sexes, in which Player I can choose A and B, and Player II can choose a and b, and what I want to do is I want to figure out the payoff from particular strategies. So suppose that P is being played by Player I and P is let's say (1/5,4/5). So what do I mean by that? I mean that Player I is assigning 1/5 to playing A and 4/5 to playing B. So suppose that Q is the mixture that Player II is choosing and she's choosing a (?,?), so she's putting a probability 1/2 on a and a probability 1/2 on b. I'm going to use P to be row's mixtures and Q to be column's mixtures.?

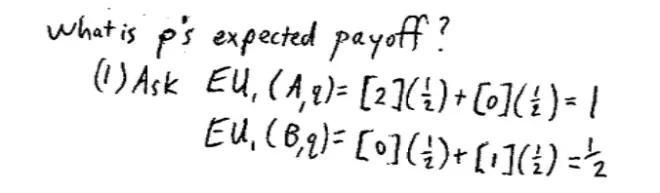
What is P's expected payoff? The way I'm going to do that is, I'm first of all going to ask what is the expected payoff of each of the pure strategies that P involves, the pure strategies involved in P. The first step is ask what is the expected payoff for Player I of playing A against Q and what is the expected payoff for Player I of playing B against Q? That will be our first question and we'll come back and construct the payoff for P.?

So the expected payoff of A against Q is what? Half the time if you play A you're going to find your opponent is playing a, in which case you'll get 2, and half the time when you play A you'll find your opponent is playing b in which case you'll get 0. So I'm going to get 2 with probability 1/2 plus 0 with probability 1/2. That gives me 1.?

Conversely, what if I played B? What's the expected payoff for the row player of playing B against Q, where Q is 1/2, 1/2? So half the time when I play B, I'll meet a Player II playing a and I'll get 0 and half the time I'll find Player II is playing b and I'll get 1. So I'll get 0 half the time and I'll get 1 half the time for an average of 1/2. And now to finish the job, I now want to figure out what is the expected payoff for Player I of using P against Q? According to P, 1/5 of the time Player I is playing A and 4/5 of the time Player I is playing B.?So to work out the expected payoff what we're going to do is we're going to take 1/5 of the time, and at which case he's playing A and he'll get the expected payoff he would have got from playing A against Q, and 4/5 of the time he's going to be playing B in which case he'll get the expected payoff from playing B against Q.?

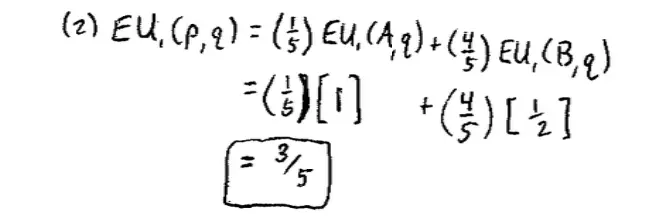
Now just plugging in some numbers to that from above, so we've got 1/5 of the time he's doing the expected payoff from A against Q and that's this number we worked out already. So this number here can come down here, 1. And 4/5 of the time he's playing B against Q, in which case his expected payoff was 1/2, so this 1/2 comes in here.?It's going to be 1/5 of 1 plus 4/5 of ?,?so I've got a total of 3/5. The number I ended up with 3/5 must lie between the payoff I would have got from A which is 1, and the payoff I would have got from B which is 1/2.?The idea here is that the payoff must lie between the expected payoffs I would have got from the pure strategies.?

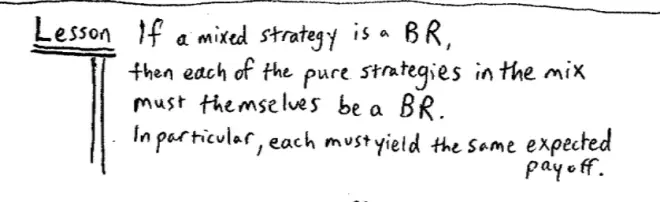
The conclusion is if a mixed strategy is a best response, if the best thing I can do is to play a mixed strategy, then each of the pure strategies which I'm playing in that mix, which I'm assigning positive probability to in that mix, must themselves be best responses. In particular, each of them therefore must yield the same expected payoff.?

So the idea here is if I'm using a mixed strategy as a best response, it must be the case that everything on which I'm mixing is itself best. And the reason is, if it wasn't, kick out the thing that isn't best and my average will go up.?

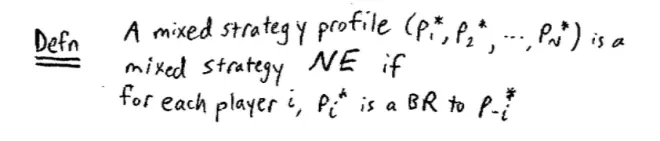
So a mixed strategy profile, (P1*, P2*, …all the way up to PN*), is a mixed strategy Nash Equilibrium if for each Player i?that player's mixed strategy Pi* is a best response for Player i to the strategies everyone else is picking P?-i*. So this definition of Nash Equilibrium, it's exactly the same as the definition of Nash Equilibrium we've been using now for several weeks, except everywhere where before we saw a pure strategy, which was an S, I have replaced it with a P.?

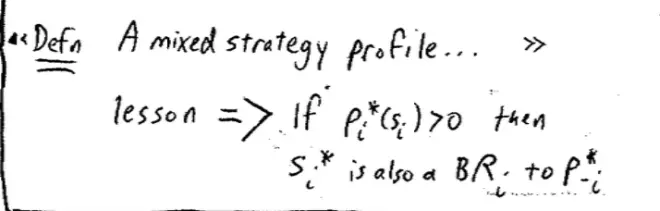
It's that if Pi* is part of a Nash Equilibrium--so if Pi* is a best response to what everyone else is doing, P-i* --, then each of the pure strategies involved in Pi* must itself be a best response. So an implication of the lesson is, the lesson implies the following. If Pi* of a particular strategy is positive, so in other words, I'm using this strategy in my mix, then that strategy is also a best response to what everyone else is doing.?

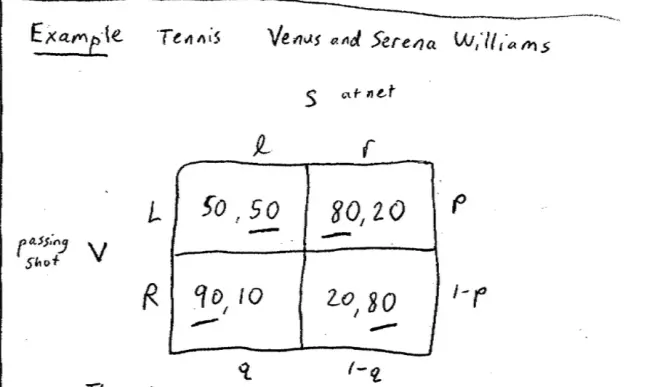
So the game within the game is this, suppose that they're playing and Serena is at the net and the ball is on Venus' court, and Venus has reached the ball and Venus has to decide whether to try to hit a passing shot past Serena on Serena's left or on Serena's right. Notice I'm going to exclude the possibility of throwing up a lob for now, just to make this manageable. So basically the choice facing Venus is should she try to pass Serena to Serena's left, which is Serena's backhand side or to Serena's right, which is Serena's forehand side.?

I'm assuming that if Venus chooses L that means she attempts to pass Serena to Serena's left, we'll orient things from Serena's point of view, and if she hits right that means she's attempting to pass Serena on Serena's right. If Serena chooses L that means she cheats slightly towards her left: not cheats in the sense of breaking the rules, but cheats in terms of where she's standing or leaning. And if she chooses right that means she cheats slightly towards her right. So this is cheating towards her backhand and this is cheating towards her forehand, assuming she's right handed, which she in fact is. So if Venus chooses left and Serena chooses right, then Serena has guessed wrong. In which case Venus wins the points 80% of the time and Serena wins it 20% of the time.?

Conversely, if Venus chooses right and Serena chooses left, then again, Serena has guessed wrong and this time Venus wins the points 90% of the time and Serena wins the points 10% of the time.?So sometimes you're successfully going to hit it past Serena but the ball is going to sail out. So that happens 10% of the time here and 20% of the time here. Look at the other two boxes, if Venus hits to Serena's left and Serena guesses left, then we're going to assume that Serena's going to reach the ball and make a volley, but her volley only manages to go in--go over the net and go in--half the time, so the payoffs are (50, 50). Half the time Venus wins the point and half the time Serena wins the point. Conversely, if Venus hits the ball to Serena's right and Serena guesses correctly and chooses right, then we're in this box. Once again, Serena has guessed correctly and she's going to successfully reach the volley and this time she gets it in 80% of the time, so Venus wins the point 20% of the time and Serena wins it 80% of the time.?

So just to finish up the description of the game here, notice that we're assuming that Serena is a little better at volleying to her right than she is volleying to her left. So this is her forehand volley and we're going to assume that that's stronger than her backhand volley. Conversely, we're assuming that Venus' passing shot is a little better when she shoots it to Serena's left than when she shoots it to Serena's right. This is her cross court passing shot and this is her down the line passing shot.?

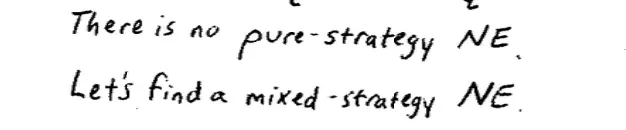
One reason it's not immediately obvious is not only is no strategy dominated here, but there is no pure strategy Nash Equilibrium in this game, in this little sub game. So if Venus--If Serena thought that Venus was going to choose left then her best response, not surprisingly, is to lean left and if Serena thought that Venus was going to choose right, then her best response is to cheat to the right, so 50 is bigger than 20, and 80 is bigger than 10. And conversely, if Venus thought that Serena was cheating a bit to the left then her best response is to hit it to Serena's right, and if Venus thought Serena was leaning to the right then Venus' best response is to hit it to Serena's left.?Maybe there's going to be a mixed strategy Nash Equilibrium.

A mixed strategy Nash Equilibrium in this game, is going to be a mix for Venus between hitting the ball to Serena's left and Serena's right, and a mix for Serena between leaning left and leaning right, such that each person's mix, each person's randomization is a best response to the other person's randomization.?

Let's assume that Serena's mix is, let's use Q and (1-Q) to be Serena's mix and let's use P and (1-P) to be Venus' mix. Let's establish that notation. So here's the trick, what should I do first, to find Serena's Nash Equilibrium mix, so that's (Q, (1-Q)), what I'm going to do is I'm going to look at?Venus' payoffs. So to find Serena's Nash Equilibrium mix the trick is to look at?Venus' payoffs.

So let's look at Venus' payoffs, Venus' payoffs against Q. So if Serena is choosing (Q, 1-Q), what are Venus' payoffs? So if she chooses left then her payoff is 50 with probability Q.?She gets 50 with probability Q and she gets 80 with probability 1-Q. If she chooses right then she gets 90 with probability Q and she gets 20 with probability of 1-Q. I meant to point to that. We're looking for a mixed strategy Nash Equilibrium, so in particular, not only Serena is mixing but in this case what we're claiming is, Venus is mixing as well. So if Venus is mixing as well, that means that Venus is using the strategy left with some probability P and using the strategy right with some probability 1-P. Since Venus sometimes chooses left and sometimes chooses right as her best response to Q, her best response to Serena, what must be true of the payoff to left and the payoff to right??

Let's go through it again, so we're going to assume that Venus is mixing. So sometimes she chooses left and sometimes she chooses right and she's going to be, she's in a Nash Equilibrium, so she's choosing a best response. So whatever that mix P, 1-P is, it's a best response. Since she's playing a best response of P and that sometimes involves choosing left and sometimes involves choosing right, it must be the case that what? It must be the case that both left itself and right itself are both themselves best response. If she's mixing between them, it must be that both choosing left or choosing right are themselves best responses. If they weren't she should just drop them out of the mix, that would raise her average payoff.

I claim this expression is equal to that expression, so simplifying a bit I'm going to get--you should just watch to make sure I don't get this wrong--I'm going to get 40Q, so this implies 40Q is equal to 60(1-Q). So I took this 50 onto this side and this 20 onto that side, so I have 40Q is equal to 60(1- Q) and that implies that Q is equal to .6.?

The trick was I found Q, which is how Serena is mixing by looking at Venus' payoffs, knowing that Venus is mixing and hence I can set Venus' payoffs equal to one another. Say that again, I found the way in which Serena is mixing by knowing that if Venus is mixing, her expected payoffs must be equal and I solved out for Serena's mix, this is Serena's mix. Let's do it again.?

Let's do the converse. Let's do the trick again, this time what I'm going to do is I'm going to figure out how Venus is mixing. I know how Serena is mixing now, so now I'm going to work out how Venus is mixing. Now, to figure out how Serena was mixing, I used Venus' payoffs. So to find out how Venus is mixing what am I going to do? I'm going to use Serena's payoffs. So to find Venus' mix, which is P, 1-P, --let's be careful it's her Nash Equilibrium mix--use Serena's payoffs. Here we go, so if Serena chooses, this is S's payoffs, if Serena chooses L then her payoffs will be what? So again, just watch to make sure I don't get this wrong and I'll point to the things to try and help myself a bit. So with probability P she'll get 50. So 50 with probability P, and with probability 1-P she'll get 10. And if she chooses to lean to the right, to lean towards her forehand, then with probability P she'll get 20 and with probability 1-P she'll get 80.?

We know that Serena is mixing, so since Serena is mixing what must be true of these two payoffs? What must be true of the two payoffs? The payoff to l and the payoff to r, what must be true about them since Serena is using a mixture of these two strategies in Nash Equilibrium? It must be the case that both l is a best response and r is a best response, in which case the payoff must be?equal.?They must be equal, these must be equal. They must be equal since Serena is indifferent between choosing left or right and hence is mixing over them. So again, using the fact that they're equal reduces this to algebra, and again, I'll probably get this wrong but let me try. So I claim, let's take 20 away from here, I've got 30P equals 70(1-P).?So I took 20 away from here and 10 away from there, and this implies that P equals .7.?

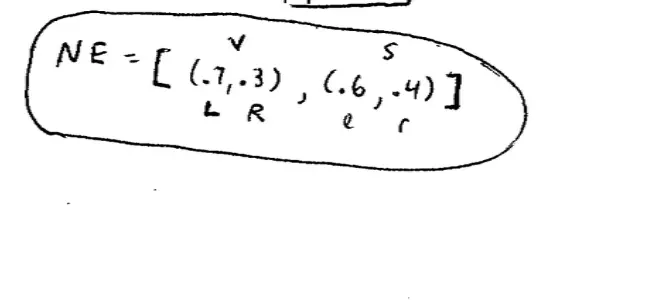
The Nash Equilibrium is as follows. This is Venus' mix. So if Venus is mixing .7, .3, .7 on left and .3 on right, and Serena is mixing .6, .4, so this is Venus' mix and this Serena's mix. Venus is shooting to the left of Serena with probability of .7 and Serena is leaning that way with probability of .6. So we were able to find this Nash Equilibrium by using the trick before.?

So suppose it were the case that Serena, instead of leaning to the left .6 of the time leant to the left more than .6 of the time. So suppose you're Venus' coach, and suppose you know that Serena leans to the left more than .6 of the time, what would you advise Venus to do? Pass to the right, exactly. So if Serena cheats to the left more than .6 of the time, then Venus' best response is always to shoot to the right. That maximizes her chance of winning the point. Conversely, if Serena leans to the left less than .6 of the time, then Venus should do what? Shoot to the left all the time. So if Serena doesn't choose exactly this mix, then Venus' best response is actually a pure strategy. Say it again, if Serena leans to the left too often, more than .6, then Venus should just go right and if Serena leans to the left too little, then Venus should always go left. We can do exactly the same the other way around. If Venus shoots to the right, so that's her cross hand passing shot more than .7 of the time, and you're Serena's coach, what should you tell Serena to do? Go that way all the time.?

So if Venus is hitting it to Serena's left more than .7 of the time, Serena should just always go to her left, and if Venus is hitting to the left less than .7 of the time, so to the right more than .3 of the time, then Serena should always go to the right. So that's how this kind of comes back into the sort of the coaching manuals if you like.?

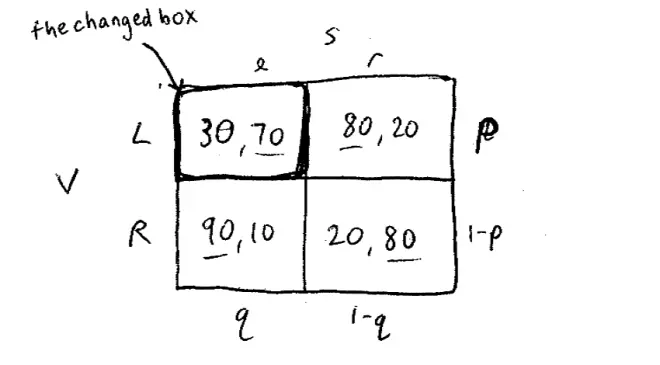
We've figured out this is an equilibrium, this is how Venus and Serena play, Venus and Serena know each other perfectly well, they know that they mix this way, they're going to best respond to it, this is going to be where they end up. But in the meantime, Serena hires a new coach and Serena's new coach is just very, very good at teaching Serena how to play at the net, and in particular, how to hit the backhand volley. So Serena's new coach, let's say it's Tony Roche or somebody, it's just a brilliant coach and Tony Roche is able to improve Serena's backhand volley and that changes these payoffs. So you should rewrite the whole matrix but I'm going to cheat. So the new game is exactly the same as it was everywhere else, except for now when Serena gets to the backhand volley, she gets in it 70% of the time. So there used to 50, 50 in that box and now it's 30, 70.?

So the game has changed because Serena has got better at hitting backhand volleys. We want to figure out how is this going to affect play at Wimbledon? Now it doesn't take much to check that there is still no pure strategy Nash Equilibrium. It's still the case, in fact even more so, that Serena's best response to Venus choosing left is to lean to the left. So it's still the case that the best responses do not coincide, there is still no pure strategy equilibrium. What we're going to do of course is we're going to find a mixed strategy equilibrium, but before we do so, let's think about this intuitively.?

I'm guessing we can't, but let's see if we can intuit an answer. So Serena has improved her backhand volley, and hence when she reaches it she gets it in more often. So one effect, you might think, is what we might want to call a direct effect and I think there's two effects here. There are two effects, one of these I'm going to call the direct effect, and by effect, I mean in particular an effect on how Serena should play the game. So since Serena has improved her backhand volley, when she reaches that volley she gets it in more often, so one might say in that case--your Serena's coach--in that case you should lean to the left more often than you did before, because at least when you get that backhand volley you're going to get it in more often. So the direct effect says Serena should lean left more, in other words, Q should go up.?

So Serena's now better at playing this backhand volley, so she may as well favor it a bit more and hence Q will go up. So that's the direct effect, but of course there's a "but" coming. What's the but??We think Serena's backhand has improved so she might be tempted to play towards her backhand a bit more often, so I claim the but is this that Venus (she's her sister after all, right, so Venus knows that Serena's backhand has improved) so Venus is going to hit it to Serena's left less often than before. So since Serena's backhand has improved, Venus is going to hit it to Serena's backhand less often than before, and that might make Serena less inclined to cheat towards her backhand because the ball is coming that way less often.?

So this is a indirect or a strategic effect. The strategic effect is Venus hits L less often, so Serena should reduce the number of times that she leans to the left because the ball is coming that way fewer times. Now notice that these two effects go in opposite directions.?One of them tends to argue that Q would go up, that's the direct effect and the other one is more subtle, it says we now think about not just how my play has improved, but also how the other person's going to respond to knowing that my play has improved, that's the more subtle effect and that's going to push Q down. That's going to make it less likely, that's an argument against leaning to the left.?

What we're going to do is redo the calculation we did before starting with Serena. So to find Serena's mix, to find Serena's new equilibrium mix, what do we have to do? The question is, in equilibrium, is Serena going to lean to the left more (so Q is going go up) or less (so Q's going to do down). So I need to find out what is Serena's new equilibrium mix. What's the new Q? To?find?Serena's equilibrium Q using?Venus' payoffs. So to find the new Q for Serena, use Venus' payoffs. So from Venus' point of view, if she chooses left then her payoffs are now, and again I should use the pointer, 30 with probability Q, this is the new Q and 80 with probability 1-Q, 30 with probability Q plus 80 with probability 1-Q.?

If she chooses right then her payoff is what? It's going to be 90 with probability Q and 20 with probability 1-Q. What do we know about these two payoffs if Venus is mixing in equilibrium? We know she's mixing in equilibrium because we saw there was no pure strategy equilibrium, so what we do know about these two payoffs since Venus is using both these strategies in equilibrium? They must be the same. Since she's using both these strategies, these strategies must be equally good. They must both be best responses so these two payoffs are equal.?

Since they're equal all I have to do is solve out for Q. So I'm going to get 90 minus 30 is 60Q, is equal to 80 minus 20 which is 60(1-Q), so Q equals .5. So what have I found out? Did Q go up or go down? Well it used to be, Q used to be what? It went down. Q went down, the equilibrium Q went down. So which effect turned out to be bigger? The direct effect of playing more to your strength or the indirect effect of taking into account that your opponent is going to play less often to your strength. Which effect turned out to be the bigger effect? The indirect effect, the strategic effect.?

Now we can also solve out for Venus' new mix and we'll do it in a second. But before I do it, let me just point out that we actually, we really can now intuit Venus' effect. It may not be exact numbers but we can intuit here. As I claim, I claim if we think this through carefully, we know whether Venus is shooting more to the left, than she was before, or less to the left, than she was before. Notice that in the new equilibrium Serena is going less often to her left even though she's better at hitting the backhand, she's better at hitting the ball when she gets there. So since Serena is leaning left less often what must be true about Venus in this new equilibrium? It must be the case that Venus is hitting the ball to the left less often.?

So to figure out what Venus is going to do, what's our trick? I want to figure out how Venus is going to mix. I'm going to find out Venus' new P, how do I find out Venus' new equilibrium mix? I look at Serena's payoffs. So if Serena chooses left, her payoff is, and I'll read it off quickly this time, is 70P plus 10(1-P) and if Serena chooses right her payoff is 20P plus 80(1-P)?and I know these have to be equal because?I know that Serena is mixing, so I know these must be equal. So since they're equal I can solve out and hope that I've got this right, so I've got 50P equals 70(1-P), so P is equal to 7/12. So 7/12 is indeed smaller than what it used to be, because it used to be 7/10, so that confirms our result.?

So the strategic effect dominated. Venus shot to Serena's backhand less often, and as a consequence, so much so, that Serena actually found it worthwhile going more to the right than she used to before. Now let's just talk this through one more time. This was a comparative statics exercise. We looked at a game, we found an equilibrium, we changed something fundamental about the game, and we looked again to look at the new equilibrium, that's called comparative statics. Let's talk through the intuition. Before we made any changes Venus was indifferent. She was indifferent between shooting to the left and shooting to the right. Then we improved Serena's ability to hit the volley to her left, we improved her backhand volley. If we had not changed the way Serena played then what would Venus have done??

So suppose in fact Serena's Q had not changed. If Serena's Q had not changed, remembering that Venus was indifferent before, how would Venus have changed her play? ?If we started from the old Q and then we improved Serena's ability to play the backhand volley, and if Q didn't change, what would Venus have done? She'd never, ever have shot to the left anymore, she'd only have shot to the right which can't possibly be an equilibrium. So something about Serena's play has to bring Venus back into equilibrium, it brings Venus back into being indifferent, and what was it? It was Serena moving to the left less often and moving to the right more often. To say it again, if we didn't change Q, Venus would only go to the right, so we need to reduce Q, have Serena go to the right, to bring Venus back into equilibrium.?

Conversely, if Venus hadn't changed her behavior, if Venus had gone on shooting exactly the same as she was, P and 1-P as before, then Serena would have only gone to the left and that can't be an equilibrium. So it must be something about Venus' play that brings Serena back into equilibrium.?It's that Venus starts shooting to the right more often.?