ECON 159.?Game Theory

Lecture?13. Sequential games: moral hazard, incentives, and hungry lions

https://oyc.yale.edu/economics/econ-159/lecture-13

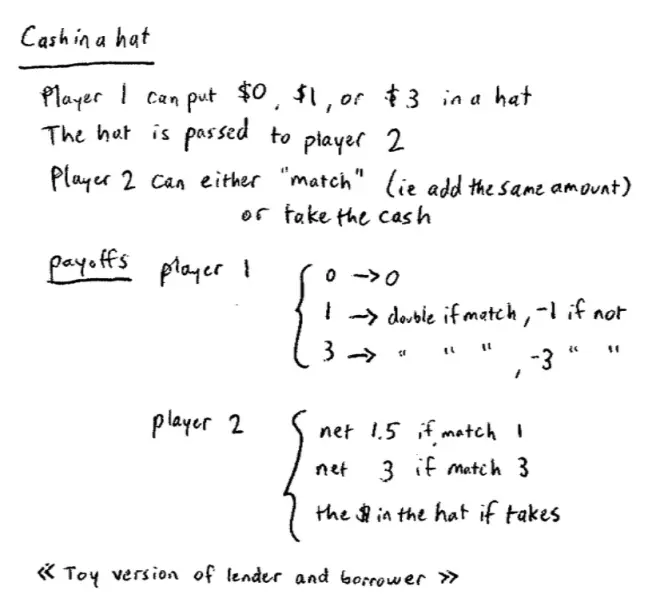
The game is going to be called cash in a hat. So the idea is this, there's going to be two players.?So Player I will have a choice, Player I can put nothing, $1 or $3 into a hat. The hat will then be given to Player II and Player?II can look at what's in the hat and either she can match what's in the hat, i.e., add the same amount in so 1 if it's 1, or 3 if it's 3, or she can simply take the cash.?

The payoffs of this game will be as follows. Player I, if they put nothing in, they're not going to get anything. If they put 1 in and it's matched then they double their money, so they get 2 back. If they put 3 in and it's matched then they double their money, so they get 6 back so they'll net 3. However, if they put 1 in and Player II takes it they've just lost their dollar, and if they put $3 in and Player II takes it they've lost $3. From Player II's point of view, if Player II matches then they get their investment back plus $1.50 if they matched 1, so the get 2.50 back in all; and they get their investment back plus $2 if they match 3, so they get 5 back in all. Of course, if they simply take the money out of the hat and put it in their pocket then that's what they get in the game.?

So once again, if Player II matches with $1, there's $1 in the hat and she matches, then she gets back 2.50 for a profit of 1.50. If there's $3 and she matches 3, she gets back 5 for a profit of 2; and if she simply takes the money out of the hat and puts it in her pocket then she gets how ever much money was in the hat.?

This is a toy version of a game involving a lender and a borrower, so you could think of our Player I's.?Imagine them working in an investment bank, or perhaps in a venture capitalist firm, and what they're doing is they're giving a loan to somebody, some budding entrepreneur who's come up with a new project.?

The lender, the guy who works at the venture capitalist firm, has to decide how much money to invest in this project. After this money has been invested in the project, the person who borrowed it faces choices. They could go forward with their project, work hard, spend the money on the things they're supposed to spend, or they could just disappear to Mexico (or go back to Yale for that matter).?

This is a sequential move game. Put the rules up here and bring this down, so for the first time we're looking at a sequential move game and we're going to spend most of the rest of the term looking at sequential move games, or at least looking at games that involve sequential elements. Now what's really, what makes this a sequential move game??What makes it a sequential move game is not simply that Player I moved first and Player II moved second, although that's true, what really made this a sequential move game is that Player II knew what Player?I had done before he got to make his move. It isn't the timing per se that matters, it's going to turn out it's the fact that Player II could observe Player I's choice before having to make his or her choice that matters.?

Notice, just while we're on the subject, more than that Player I knew this was going to be the case. So let's just get that down. So in this game Player II knows Player I's choice before she chooses--she being Player II, let's say before II chooses. Second, Player I knows that this will be the case, and the way we dramatized this just now is Player?I put the money in the hat, the hat was transported across the classroom with people very honestly not stealing the money to Player II, Player?II could look in the hat, could see how much money was in there, before Steven or Nate had to make that choice.

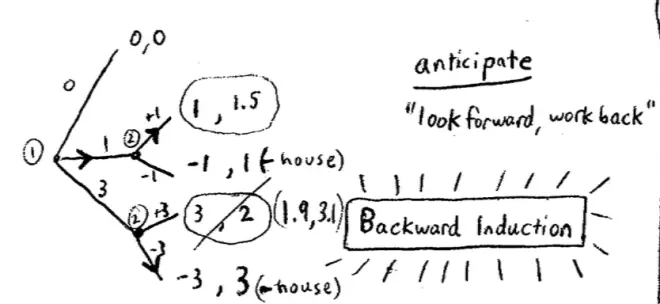
So how do we go about analyzing games that have this sequential structure? So it turns out that a useful way to analyze them, and the way I want to get us used to today already, is to draw a tree. So in the first half of the class we drew a lot of matrices, now we're going to draw trees. For those people who haven't seen trees before, not a big deal. It's an object that looks like a tree, that's why it's called a tree. So let's have a look, so in this particular game, here is Player I making her choice and in fact she has three possible choices. She can put nothing, 1 or 3 into the hat. Player II then chooses, although really Player II only has choices to make if there's some money in the hat, and Player II has two choices in this particular game in either case.?

Either Player II is going to add $1 or $3 into the hat or they're going to disappear off to Mexico, taking our investors' lunch money with them. Let's put down the payoffs. So let's put down as payoffs, the net gains they make. So if nothing goes in, no one makes any money so (0, 0) will be the payoff. If 1 is matched by 1 then the investor, the lender doubles her money so she makes a net profit of 1. If the money is taken out by Player II then she loses 1. Down here if II matches her investment of 3 she doubles her money again, so she makes a net profit of 3, and if the money is taken out she loses 3. Everyone all right with that? Let's do Player II's payoffs. In the case in which he matches 1 he makes a net profit of 1.50. In the case in which he just steals the 1 he makes a net profit of 1. And down here, in the case where he matches 3 he makes a net profit of 2--he gets 5 back but he'd invested 3 to start with --, and here if he just takes the money out he makes a profit of 3.?

So the idea here is that the players who move early on in the game should do something we've always talked about before. They should put themselves in the shoes of the other players, but here that takes the form of anticipation. They're anticipating what players down the tree are going to do. So the key idea here is anticipation. What they're going to do is they're going to look forward down the tree; imagine themselves in the shoes of the later players; look at the incentives facing those later players; imagine that they do the best they can--those later players do the best they can --; and then walk backwards through the tree.?

So the key idea here is to look forward to the end of the tree and work back: look forward and work back. So let's imagine ourselves in Steven or Nate's shoes, having found--as they did in fact--having found $1 in the hat. They then are making a choice between adding $1 which nets them a $1.50 or taking the $1 which nets them $1. 1.50 is bigger than 1, so we think they're going to go this way. Everyone happy with that? Conversely, if they found themselves with $3 in the hat then, if they add $3 --they match--they're going to get $2, they're going to net $2; and if they take the money out they're going to get away with $3. 3 seems bigger than 2 so we think they're going to go this way.?

Again, we're assuming that these are their real payoffs. Okay, so from Player I's point of view, since Player I knows that Player II will observe the choice before making her own choice, and since Player I can put him or herself in Player II's shoes and anticipate this choice, Player I is essentially choosing between what? If she puts in 0 she gets 0, if she puts in 1 she knows II will match and she'll double her money and get 1, and if she puts in 3, then she knows Player II will take the money and run, in which case our lender will have lost $3. So she's choosing between 0, 1 and -3 and she's going to choose $1, which is exactly what happened in the game. Everyone happy with how we did that??

So this idea of starting at the last player, the player who moves last, solving out what they're going to and then working our way back through the tree has a name. The name for this is "backward induction."?

What keeps the economy running is the ability of lenders to lend money to businesses that then invest them profitability, and are able to make returns. So this underlies a whole bunch of stuff going on in the economy. So let's talk about this and the first thing I want to talk about is, I want to point out that there's a problem here. There's a bad thing here, much like there was a bad thing in the very first class of the semester. In the very first class of the semester the bad thing was a Prisoner's Dilemma, but here it's a little different but let's focus on it a while.?

So the bad thing is we ended up here. Not a disaster: the lender doubled her money. The borrower was able to go ahead with the project on a small scale and make some money. The bad thing, however, is that we would have liked to end up here. Had we been able to have a large project funded with $3 and had the borrower repaid those dollars, so matched in effort or whatever that happens to be, then we'd have ended up at an outcome that is better not just for the lender--it's obviously better for the lender--but it's also better for the borrower. So the outcome we would like to have reached gets the lender 3 whereas she's only getting 1 where we ended up, and it gets the borrow 2 where he's only getting 1.50 where we actually ended up.?

So the problem here is Katie would like to invest 3 if she knew that in fact Steven was going to match, but she knows Steven's not going to match. Steven, in fact, is going to run off with the cash. It's going to end up being spent at Starbuck's or something. From Steven's point of view he would actually like to be able to borrow the $3. He would like to be able to end up at this 3, 2 outcome as well. The problem is he knows that Katie knows, and Katie knows that he knows, that in fact he's going to run off with the cash. We'd like to get this good outcome but incentives are preventing us from getting there. What do we call this kind of situation??

This is called "moral hazard." The agent, in this case the borrower has incentives--will have incentives--to do things that are not in the interests of the principal. If we're not careful, for example, by giving too big a loan, the incentives of the borrower will be such that they will actually not be aligned with the incentives of the lender and that will prove to be bad for the lender. But notice the existence of this moral hazard problem isn't only bad for the lender. It ends up being bad for the borrower as well. Let me give you another example, in insurance there's a classic, probably the classic moral-hazard problem.?

If an insurance company insures me against having my car stolen, there's a moral hazard problem in that I might, if the car is fully insured, I might now have the incentive not to bother to lock my car or to leave it anywhere on the street in New Haven, because I'm not bearing the cost. So the insurance company needs to worry about that in writing an insurance contract for me. And in practice what the insurance company does is it forces me to take a deductible. It doesn't allow me full insurance. It makes sure that some of the cost of having a car stolen is going to fall on me. That's bad for me by the way because it means I can't get full insurance. And notice that what happened here is rather similar.?

In this case, both the lender and the borrower would rather have a big project, a big loan, and have the agent pay back that loan. They'd prefer this (3, 2) outcome, but they can't get there. And therefore rather than having a full scale project, Katie or Justin only offered the borrowers a small scale project. So the idea here in this example was--what happened was we kept the size of the project or the size of the loan--you can think of this as the project if they're borrowing something--small to reduce the temptation to cheat, to reduce the temptation not to repay the loan. So these problems are all over society but they're particularly prevalent in situations involving lenders and borrowers.?

A lot of you are about to go out and try and borrow money to set up your projects, run your new version of Facebook or whatever. And a lot more of you as we said before, are going to end up loaning money, perhaps someone else's money probably, at least for a while. And we want to know how you might solve this moral hazard problem. We've seen one way to solve it.?One way is for me to keep the size of the?project?small.?

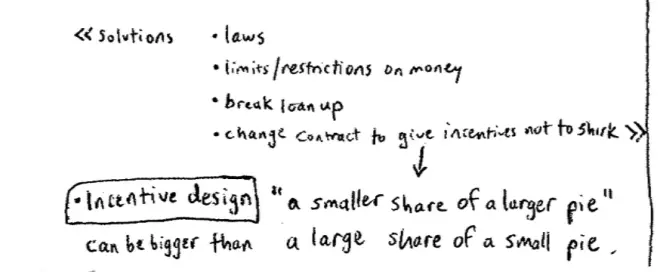
We could impose laws. Okay, so we could impose laws much like we tried in the Prisoner's Dilemma, we could regulate this market. There's going to be a little bit of a problem we're going to run into in regulating the law, in using the law here. What's the problem we're going to run into here? We do have laws that regulate borrowers and lenders. What's the law that regulates borrowers and lenders: bankruptcy law.?So we have law that regulates to some extent what lenders and borrowers can do. One of the things that we do in that law is we limit the degree to which we're allowed to punish the borrowers. So bankruptcy law pretty much says we're going to put some limit on how much Katie can inflict pain on Steven for running off with the lunch money. Steven can simply say I can't repay, I'm bankrupt, and he's more or less allowed to have a fresh start.?

So you could try and say there's only certain things you can do with the money. And, for example, to make that credible, what you might have to do is to say: show me what you're going to do with the money, show me the receipts. Or another thing you could say is, I will only give you the money if you show me exactly how you're going to spend this. That's a good solution. Notice that you could regard that as changing the order of play. It's a little bit like saying, let's have the borrower have to move first, let's have the borrower have to commit what their actions are going to be, how they're going to spend the money before--you know--show the contracts before the lender lends them the money. That's a good solution, but again there are limitations to this solution.?

One problem is just sheer lack of flexibility. If, in fact, the entrepreneur is not going to be flexible on how they actually run the project, there's not much point of being an entrepreneur in the first place. There's a limit to how much control you want to give to the lender. The lenders don't really want to run the project for you. There's also a severe problem of timing. It's simply not going to be possible to specify all the expenditures of a project up front. You're going to need some money to do some things ahead of time. So it's a good idea--changing the order of play is a good idea--but there's going to be limitations to this.?

One possibility is to break the loan up and give it--let it come in small installments. If you do well on the first installment I'll give you a bigger installment next time. Notice that that's a little bit like something we talked about in the very first week. It's a little bit like taking this one shot game and turning it into a repeated game. It's turning a one shot interaction into a repeated interaction. We'll come back and talk about repeated interactions later on in the course. Again, notice that there might be some limitations to this. I mean I think it's a good idea, and in general you should be trying to do this, but it could just be that the set up--for Nate to set up his new Facebook and for Steven to set up his new mousetrap factory--they just need a chunk of money at the beginning. There may be some limit to how little money you can give them at the beginning since they have to hire workers, and set up the factory, and make some big splash in advertising, and so on and so forth.?

So what you could do here is you could redesign the payoffs of this project in the event that it's successful. What you could do is take these 5 units of profit and instead of having (3,2)--let's write that in a different color--we could give the borrower, the entrepreneur 3.1, leaving 1.9 to the lender. All right, so we could change the payoffs of this contract to be (1.9,3.1) in the event of a big project. Because now our borrower, Nate or Steven, were they to end up with a hat with $3 in it, they now will find it in their interest to match the $3 and get 3.1 rather than 3.?

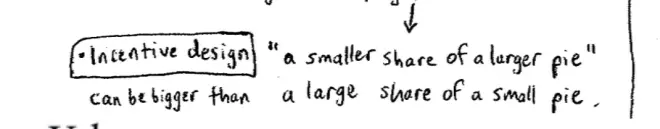
This idea of changing the contract to give the borrower incentives to repay, incentives not to shirk, incentives not to disappear with the cash, is an example of what's called "incentive design." So the idea here is, in a lot of businesses, incentives are not given by God. They're designed by the people who write the contracts. If you're either the borrower or the lender, you should be thinking about writing a contract that's going to achieve the end that you want. Now notice in this particular example, exactly as Nate said, the lender's going to take a bit of a hit here, they're not going to get a 100% return, but they're ending up doing better than they would have done by giving a small loan. They've ended up getting 1.9 rather than 1, so in this particular example--it won't always be the case but in this example--they're taking a smaller share of a larger pie.?

Sometimes a smaller share of a larger pie is bigger than a larger share of a smaller pie: not always but sometimes. The reason the pie is larger is we're able now in an incentive compatible way--we're able to go ahead and have a large project. So in this example, the smaller share of the larger pie actually ended up being bigger than the larger share of the smaller pie. So a smaller share of a larger pie can be bigger than a large share of a small pie, not always of course. This is just an example. Now let's just be a little bit careful here. So in this particular example, even though this 1.9--this return that our lender is able to make by accepting a smaller share of a larger pie--even though it's a bigger absolute return, it's smaller in another sense.?

So CEO's have huge incentive clauses in their contracts, sometimes in the form of options. Why do they have those incentive clauses in their contract? Well there's two interpretations of this. One interpretation is, it's just a bad thing and they're just trying to screw the world. But there's a more moderate view of this. The more moderate view of this is that those incentive clauses in their contracts are attempts to align the interest of the managers with the interest of the shareholders, just as this contract is attempting to align the interest of the lender and the interest of the borrower. So by managers I took him to mean CEOs, but what other kind of managers recently in the press, very recently, this weekend, have been talking about incentive contracts??

Managers of sports teams also have incentive contracts these days: incentives to achieve certain levels. Here it's not quite clear to me exactly what's going on. We call those incentive contracts but you might want to worry a little bit. I mean do we really think that the manager has an incentive to lose otherwise? So part of what's going on with incentive contracts isn't actually incentive contracts, part of it is about sharing the risk. Particularly in the kind of contracts that have been written about over the weekend with Joe Torres' contract for the Yankees, which he turned down, is partly perhaps to give him incentives to try and win, but perhaps it's more to do with sharing the risk among the general manager and the manager of the team if they don't make it to the playoffs.?

But all right, they're still incentive contracts and we see incentive contracts elsewhere, and we've seen them since the Middle Ages. So in the Middle Ages, incentive contracts took a particular form, and the form was called two things, piece rates and in agriculture it took the form of share cropping. So share cropping is a contract whereby part of the output of the farm goes to the landowner and part is kept by the farmer. Going back to the Middle Ages, part of the output would stay with the peasant and part of it would go to the lord of the manor. Piece rates are a similar idea. Rather than paying wages to workers, just bundles of cash, the amount which they're paid depends on output. So piece rates would say if you produce seventeen yards of cloth then you'll get paid the revenue that's derived from three of those. Both of these forms of contracting are there partly to create incentives. They create incentives because they create the incentive for the farmer to increase yields and they create incentives on the part of the worker to increase output. So piece rates are a big part of the story.?

Sometimes having lower payoffs can actually make you better off, and the reason it makes you better off, is it changes the behavior of other players in the game in such a way as may benefit you; in this example, by inducing the lender to give you a bigger loan. So the way the collateral works is it lowers your payoffs if you do not repay, but it leads to you being better off. The reason it makes you better off is it changes the choices of others in a way that helps you. We're going to see lots of examples of that in the next couple of days. Now collateral is an example, we talked about incentive design, collateral is also an example of something larger. The larger thing is the idea of commitment. Collateral is a commitment strategy. It commits you to repaying the loan.?

I want to give another example of a commitment strategy. I think this idea of commitments is an important one, and we have just about time to do it. So I wanted to go completely away from our context of our lender borrower game a second and look somewhere else entirely, so we get rid of this for now. I want to take us back to 1066, what happened in 1066? The Norman Conquest took place in 1066. So the Norman Army invades from Normandy led by William the Conqueror and lands on the Sussex beaches at Hastings. What I want to imagine is a game involving the Norman Army, or William the Conqueror in particular, and the Saxon Army.?

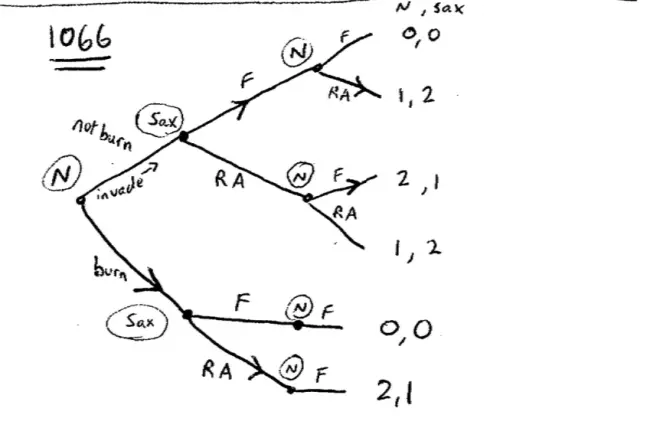
So here's the little game. So we're in the area of medieval military strategy, and here is the game. We'll start with the Saxon's here, the Norman's have already invaded, so I guess the Norman's have already moved but here's the Saxon Army making a decision. They're deciding between fighting and the important medieval military tactic known as running away. Of course the Normans are going to know whether the Saxons are actually going to charge down the beach and attack them, and they are going to have to decide whether to fight or run away. Let's put the payoffs--now leave some space below here, leave some space down here on our notes--let's put the payoffs in. So I'm going to put the Norman payoffs first and the Saxon payoffs second. Norman payoffs first, Saxon payoffs second.?

Now this is probably the classic example of a commitment strategy. William the Conqueror, in this example, or Cortez in perhaps the more famous example, burned the boats to get rid of some strategies, to get rid of some choices altogether. And you might think how can getting rid of choices make me better off? The reason, in a game, particularly in a sequential game, in a game generally, the reason getting rid of choices can make me better off is it changes the behavior of people on the other side of the game in such a way as benefits me. In this particular example, it makes the other side less likely to fight. So once again this is a commitment and the way it works is--this example of a commitment is actually to have fewer options and it changes the behavior of others. If it didn't change the behavior of others it wouldn't be worth doing.?

So the worry that the Soviets have is they think the Americans might attack them, and they worry that the Americans might attack them thinking that they won't retaliate, because they won't really have any incentive to retaliate once their cities are destroyed. So they construct a device they called the doomsday device that will automatically launch nuclear missiles back on the Americans if the Russians are attacked. It's a commitment device to make it credible that they will actually respond were they to be attacked by the crazy Americans. So there's a mistake, however, that the Russians make. What is the mistake that the Russians make??

They don't tell the Americans that they've built the doomsday device. So this is really an important idea hidden in what's really a great movie. Commitment strategies are a good idea. They can make things credible. But the only reason that having fewer strategies is good for you is because it changes the behavior on the other side. In this case, it changes the behavior of the Saxons. It doesn't work if the other side doesn't know about it. It's crucial that the other side knows. So the other players must know.Just to hammer this home, notice that the expression in the English language is "burning your boats." It's not "going over to your boats and quietly drilling a little hole in them," it's burning your boats. You want the other side to see this big bonfire on the beach and to know that the boats are no longer available. Just as in Dr. Strangelove, it's crucial, and it's a terrible mistake for the Russians not to tell the Americans that they've built this machine.?