By: Tao Steven Zheng（鄭濤）

Rene Descartes (1596 - 1650) found the theorem without proof and sent it to Princess Elizabeth of Bohemia in 1643. The theorem was first proven by Jakob Steiner (1796－1863) nearly 200 years later in 1826. In Edo Japan, this theorem first appeared in a sangaku problem from 1796. The theorem was explained in Hashimoto Masataka's book ''Sanpo Tenzan Shogakusho'' (筭法點(diǎn)竄初學(xué)抄) in 1830.

【Problem】

Suppose there are four circles? lying in a plane, such that each circle is mutually tangent to the other three circles. Let the radius of each circle be . Prove that

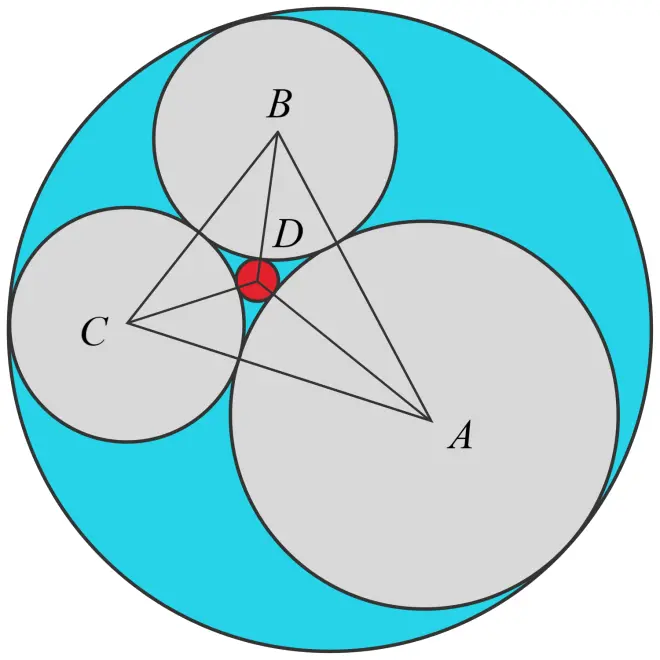
Hint: Given three angles? where , then .

【Solution】

Let , , ,? ,? , and .
?
Furthermore, let there be three angles , , and .

By applying the cosine law on triangle ADB, we get

Expanding each bracket and rearranging yields

Solving for? yields

Using the same method, we can also obtain

Let

Using the trigonometric identity from the hint gives

Expanding and rearranging the above equation yields

Divide both sides of the equation by :

Replace the variables for?? in terms of?:

Expand the left-hand side of the equation:

Expand the right-hand side of the equation:

Subsequently,

Divide both sides by :

Add? on both sides:

This can be compactly expressed as

Additional Remark

Solving the result for? gives two solutions, one of the incircle (inner circle) and one for the excircle (outer circle).

Incircle radius

Excircle radius