GG 140: The Atmosphere, the Ocean, and Environmental Change

Lecture 12.?Circulation of the Atmosphere (Exam I review)

https://oyc.yale.edu/geology-and-geophysics/gg-140/lecture-12

Review of Exam Solutions [00:00:00]

Question one was about computing the total mass of Venus' atmosphere. And we're going to use the same principle we used to do the Earth's atmosphere in class. We use the hydrostatic relation for the full column, which says that the pressure at the bottom of the column is balancing the weight of the air above it. So by looking at the ratio of pressure to gravity, you can get the mass per unit area in a column of atmosphere. And then just multiply that times the surface area of the sphere.

Question two was about water vapor. It had two parts, first to compute the partial pressure of water vapor. And I gave you the density--the mass density of water vapor, and I gave you the temperature. So you should have used the perfect gas law for that. The partial pressure for water is the density for water times the gas constant for water times the temperature.

And you're given 0.01 kilograms per cubic meter for the density, but now you've got to be assured you use the right gas constant. So the gas constant for water is going to be the universal gas constant, 8,314, divided by the molecular weight for water. Water is H2O. The molecular weight of oxygen is about 16. The molecular weight of each hydrogen atom is 1, so that adds up to 18.

The relative humidity is the ratio of the partial pressure of water vapor to the saturation value at the temperature that you have. And there's a table here that gives you a few values for saturation vapor pressure for water at given temperatures. And for 20 degrees, it's 23.4 millibars. Got to keep consistent units. We're working in Pascals, so I divided by 2,340, and I get 0.58, which is 58%.

The greenhouse effect, why does it warm rather than cool the surface of the planet? The point is that the greenhouse effect has to do with atmospheres absorbing some fraction of the radiation that's trying to penetrate through it.?It turns out that it's easier for the Sun's rays to get in than it is for the Earth radiation to get out.

If it were the opposite, then I suppose the greenhouse effect would be a cooling mechanism, making it difficult for the Sun's rays to get in. But if it's easy for the Earth's radiation to get out, that probably would cool. But it doesn't. So easy to get in, difficult to get out, therefore, the Earth's temperature must warm in order to reach that radiative balance.

So what makes it easier to get in than to get out? It's not the direction. It's the wavelength. The wavelength of the radiation coming from the Sun is centered around--in the visible range, about 0.4 to 0.7 microns. And because of the gases we have in the atmosphere, the particular gases, the atmosphere is mostly transparent to those wavelengths. On the other hand, the Earth's surface being cooler, when it radiates, it radiates at a longer wavelength. And for those wavelengths, the atmosphere is mostly opaque. So that's why the greenhouse effect is there. And quite a few of you had a garbled explanation of that.

What gases contribute and why? So it turns out that none of the molecules we define as being air molecules--that is, N2, O2, and argon--none of them are active greenhouse gases. Their structure is too simple. They don't have a dipole moment, and they cannot absorb or emit the infrared radiation.

But slightly more complex molecules, like CO2, water vapor, ozone, N2O, NO, they have enough of a complex structure--mostly asymmetry. They break symmetry in a way that allows them to have a positive-charged end and a negative-charged end. And that means that they've got a dipole, and they can--just like your cell phone, they can emit and they can absorb radiation using that oscillating dipole.

Question five, a small rocky asteroid.?I give you the solar constant--that's how much radiation is reaching that--and I give you its albedo. So if you've got this little asteroid, it's got a certain value of the solar constant. It's going to be different for Earth, because it's closer to the Sun, so the solar constant's going to be a little bit larger.

You've got to make the same assumption we made in class. You're going to have to assume that you’ve reached some kind of a steady-state temperature, where it's receiving an amount of radiation per unit of time and emitting at the same rate to space. And then you've got to find the temperature of the object that allows it to be in that steady-state balance. If the temperature's too cold, it won't be radiating enough to be in steady-state. If it's too hot, it'll be radiating too much to be in steady-state. So there's only one temperature that'll allow it to balance its heat, and that's the one that you can derive from this formula.

So solar constant, 1 minus the albedo, over 4 times the Stefan-Boltzmann constant. So 2,000 watts per square meter, 1 minus the albedo, 4--there's the Stefan-Boltzmann constant--take the fourth root, 257 K.

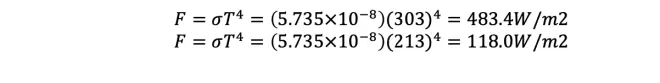
Question seven was?a cloud. The earth is radiating, and the cloud top is radiating. The temperature of the Earth I gave you as plus 30, and this was minus 60. And I just asked you to compare how these two surfaces are radiating to space. The two things you had to do, you had to compute the wavelength that was being most strongly emitted by each surface. Each surface emits a broad range of wavelengths, but there's a peak where it emits more than at other wavelengths. And that's given by Wien's Law.

So for the higher temperature--this is the constant divided by the temperature in Kelvin--it comes out to be 9.56 microns. And for the cooler temperature, it's at about 13.6 microns. But both of those fall into the thermal infrared range of radiation. And in terms of the flux, how much radiation is being emitted, it's the Stefan-Boltzmann Law. Again, put in the temperatures in Kelvin, and you get 483 and 118. A big difference arises because of that powerful power of four in the exponent there.

Question eight?was one of those release of a pollutant in an unconfined atmosphere with no wind. It says there's no wind blowing. So I imagine a source that's diffusing out in all three directions--north, south, and upwards--forming a growing hemisphere of polluted air. And the radius of that hemisphere is growing with time according to the square root of the diffusivity times time.

And then this concentration we're looking for is the mass of the pollutant divided by the mass of the air into which it has been mixed. And I said you put in 10 tons, I think, so that's 10 to the fourth kilograms divided by 2.8x109?kilograms, just this number brought down, and I got 3.57x10-6. In mass units, kilograms per kilogram. So noticing the minus six, I could write that as 3.57 parts per million--there's the million--by mass. By mass because it's kilograms per kilogram.?

Differential Heating and Earth’s Energy Balance [00:23:06]

I want to start a new subject today, which is the general circulation of the atmosphere.?So we just finished a big section on water in the atmosphere, so this is a new topic now. We're going to look at the whole globe and try to understand the large-scale air motions on the globe.

The basic principles that are going to control how we think about this problem is that differential heating generates the circulation. Now, you know this. If I have a bonfire over here or a hot stove or something, it's going to heat the air near it. That warm air wants to rise because of its buoyancy, and you're going to set up a circulation in this room driven by the fact that you're heating the air here but not there. Differential heating means you're applying different heating at different locations.

But that circulation?is going to move heat--because the air carries heat with it, it's going to move heat from hot to cold regions trying to balance out the local heat budgets. So we're going to see this principle applied now to the atmosphere as a whole.?Here's the globe, and the Sun hits the equatorial regions most directly. In the equatorial regions in the middle of the day, the Sun is directly overhead. So this cosine theta factor is about one. You're getting the full intensity of the Sun, 1,380 watts per square meter, directly hitting regions near the Equator.

And it turns out that there's less thermal radiation being emitted in the equatorial regions than is being received from the Sun. So while we assumed a week or so ago that the Earth as a whole is in radiative balance, that is not true for each latitude belt. Each latitude belt is out of a state of radiative balance. As I've shown here near the Equator, getting more from the Sun than it's emitting to space, and at the poles, where the radiation is coming in tangentially, you're really getting very little sunlight.

Of course, with the tilt of the Earth, you do get a little bit, but let's assume that ray is just parallel here. It's just going to hit the North Pole tangentially. It's not going to deliver any solar energy that way. But the temperature of the pole is not absolute zero, so it will be radiating to space.

So there's an imbalance here. There's an excess of heat near the?Equator and a heat deficit near the poles. How can that be sustained? The way that is sustained is to have some other mechanism for transporting the heat from the Equator to the pole. And that's where the general circulation comes in. So not only is the difference in heating going to produce a circulation by buoyancy forces, but that circulation then is going to solve this problem we have of how to balance out the heat budget at each latitude.

So there's two ways to look at this problem. Differential heating causes the circulation, and the circulation helps us to balance the heat budget at each latitude. I'm going to go through this now in some detail, because this is the key concept for understanding the Earth's general circulation.

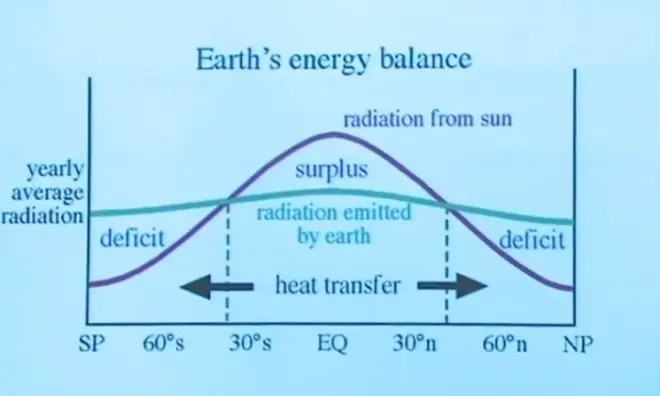
So on the x-axis is latitude from the North Pole down to the Equator to the South Pole. And there are two curves here. The red curve is radiation received from the Sun. That could be over a day or over a year, averaged out. But anyway, there's a lot of radiation being received from the Sun in the equatorial region and much, much less at the poles.

Now, that's probably an annual average. And during Northern Hemisphere summertime with this tilt, and?there is a little bit of radiation received at the pole. In the Northern Hemisphere winter, there's absolutely none. So you don't get a zero value. You get something that's an average of the seasons. But it's definitely much less than what is received at the Equator, just because of the geometry of the sphere. It's nothing more than just the geometry of the sphere and the fact that the Sun's rays are coming in parallel to each other.

Now, the equatorial regions are warmer than the other parts of the planet, so they radiate more by the Stefan-Boltzmann Law.?The hotter the surface, the more it radiates, but not enough to make up that difference. So there is a heat surplus near the Equator. Near the poles, it radiates less than at the equator, but not so much less that it doesn't leave a deficit there.

Poleward Heat Transport [00:29:57]

So we've got this problem of how to balance the budget in the Equator and in the high-latitude regions. And that is done, as I've said before now, by a heat transfer mechanism that has to do with the ocean and the atmosphere transporting heat to the poles to balance out that heat budget.

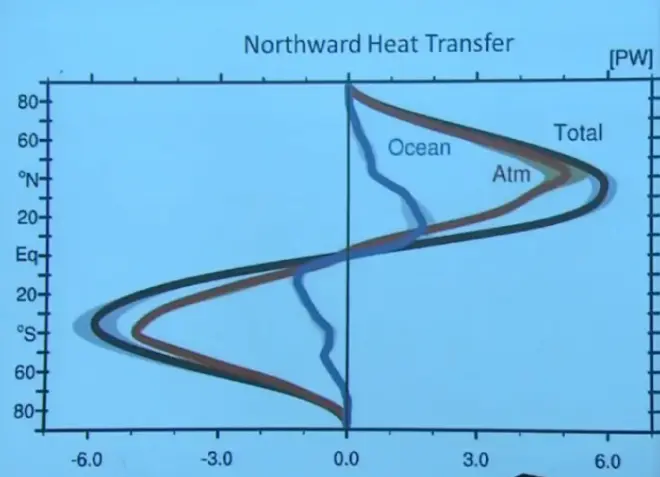
So here's what we estimate from what we know about the atmosphere using balloon soundings and so on to work this out. What's plotted here on the x-axis is the heat transport in watts--it's a power unit--as a function of latitude. North Pole, Equator, South Pole. And the total is shown in the black curve, the atmospheric component in red, and the ocean in blue.

Now, something about the units. It says capital P, capital P capital W up there. The capital of the P means "peta." You know the prefixes "kilo" and "mega" and "giga" and "tera." You keep going up till you get to peta, which is 10 to the 15th. So a petawatt is 10 to the 15th watts. So for example, at a latitude of about 30 or 40 north latitude--and New Haven is right here at 40 north, just about in the peak of this curve--there is about six petawatts of energy being transported towards the North Pole by ocean and air currents in the atmosphere. Most of it's by air currents.

From your experience, you know that on days when it's especially warm, the air is blowing from the south, typically. On days when it's especially cold, the air is blowing from the north. So there's this transport of air back and forth.

You have roughly the same amount of air moving north and south, but when?it's blowing northward, it's carrying more heat, because it's hotter. And when it's flying southward, it's carrying less heat, because it's colder. So just from that asymmetry that you would notice on a day-by-day basis, you can understand what's causing this north-south heat transport. It's just air moving back and forth, but carrying more heat on its way north than it does on its way south.

I'm going to illustrate that first for the ocean. This is a crude diagram of the gyres in each of the world's ocean basins. For example, in the North Atlantic gyre, there is a warm current going northward. That's the Gulf Stream, shown in red to indicate that it's a warm current. There's a cold current running southwards.

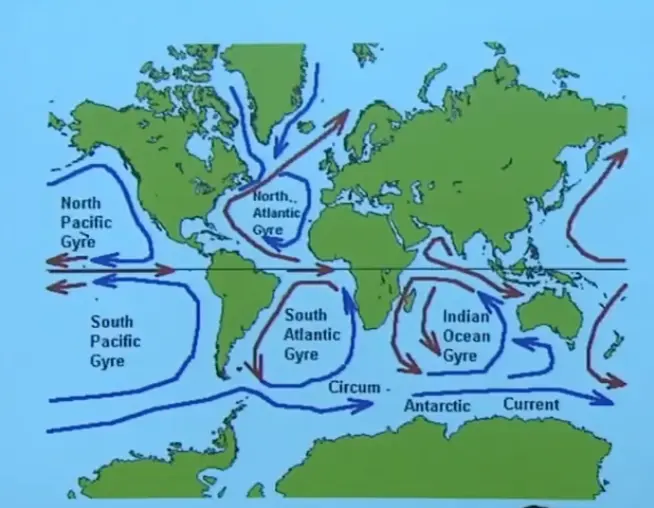
You're taking the same amount of water north and south. You're not piling up water at the pole or at the Equator, but you are transporting a net amount of heat--not a net amount of water, but yes, a net amount of heat. Because the water going northwards is warm. The water moving southwards is cold. So they don't balance each other out in terms of the heat that they're carrying.

And the same thing goes on in the Southern Hemisphere. For example, there are warm currents and cold currents, so the net heat transport is towards the south. That's why they plotted this negative on the last plot. So if we call this plot the northward heat transport, it's positive in the Northern Hemisphere, because you're transporting heat towards the North Pole. It's negative in the Southern Hemisphere, because you're transporting heat towards the South Pole, going in the opposite direction, so we give it a negative sign like that.

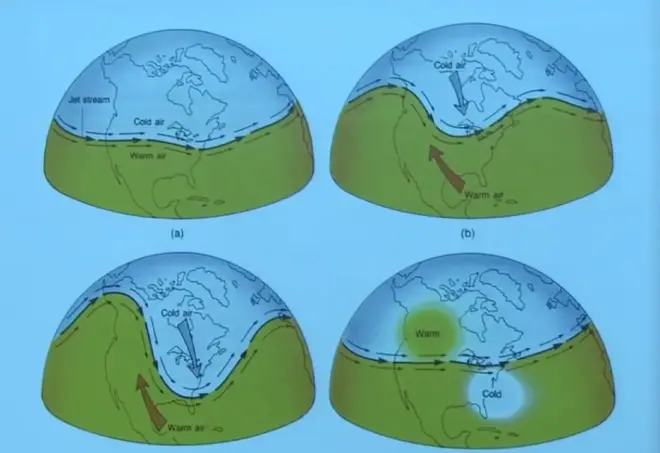
So the oceans are doing some of it, but the atmosphere does most of it. Typically, if you have warm air and cold air and the jet stream is running around the Earth kind of in a zonally symmetric fashion, well then, you're not transporting any heat. But very frequently, it'll break down into a wave-like motion, where cold air will come streaming down--in fact, here's New Haven right about here--cold air will come streaming down from the pole, heading to the Equator. That has to be replaced by an equal amount of warm air moving poleward. And in so doing, you'll have a net amount of heat transported towards the pole, and that's what'll balance out the heat budget at each latitude.

Heat Flux by moving air [00:35:08]

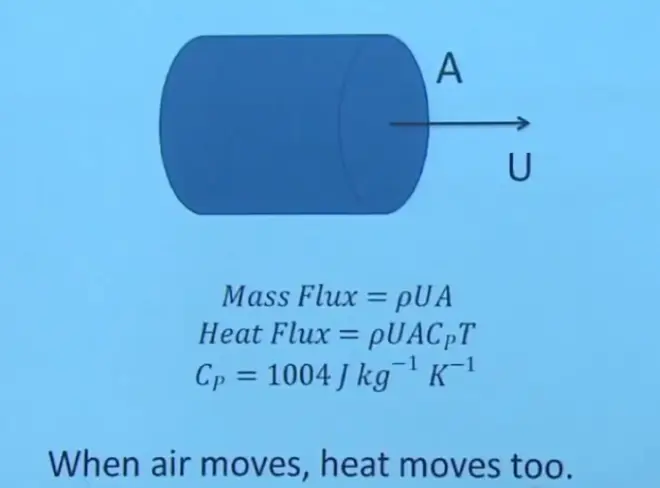
Just to remind you about this basic physical principle, if you imagine a pipe carrying a fluid, what do you know about the pipe? You probably know the cross-sectional area of the pipe, you know the speed of the fluid in the pipe, and you probably know the density of the fluid in the pipe. Then if you wanted to know the mass flux--how much water or how much air is being carried by that pipe--it's simply the product ρ*U*A, and that'll have units of kilograms per second. That'll be a mass flow rate.

It's only a small step to go beyond that to understand how much heat is being transported in the pipe. Because we know the heat capacity, or the heat stored in a fluid, is proportional to the mass that you have times the specific heat capacity times the temperature. So this quantity Cp,?the specific heat capacity at constant pressure.?The units here are joules per kilogram per degree Kelvin.

So the more mass you have, the more heat is stored. And the hotter the temperature, the more energy is stored in a particular kilogram of air. So to go from the mass flux to the heat flux, you just have to multiply by these additional two factors, the heat capacity, which is the amount of heat you have per degree of temperature, and then the temperature itself.

This doesn't quite convey the full picture I want to convey. If I went back to this picture, what I'd like you to envision is two of these pipes. One's carrying air southward, and the other is carrying an equal amount of air mass northwards. The amount of mass flow in each pipe is the same, but the amount of heat flow is not, because the temperature is different for the two pipes.?So no net transport of mass, but yes, a net transport of heat. Because one stream of air is cold, and the other stream of air is hot. So I don't think this is a particularly difficult concept, but it lies at the base of understanding how the atmospheric general circulation works.

Effect of Earth’s Rotation: Coriolis Force [00:39:19]

Now, the subject gets a little more complicated?because of the effect of the Earth's rotation. I'm talking about the Earth spinning on its axis. It distributes the Sun's heat zonally. Because the Earth is spinning on its axis, it's not a hot spot that forms, but a hot region near the Equator that forms. The spinning of it distributes the Sun's heat zonally. We use the word "zonally" when we're going this way around the Earth. And you end up with a latitudinal--or sometimes we say "meridional"--temperature gradient, or heating gradient. But zonally, the heat gets well distributed because of the spinning of the Earth.?

We'll get to next week is the Coriolis force. Whenever a planet spins, it generates a somewhat mysterious new force called the Coriolis force. Whenever a parcel tries to move in a straight line on a spinning planet, it gets deflected. And that really has a major influence on the nature of the general circulation.

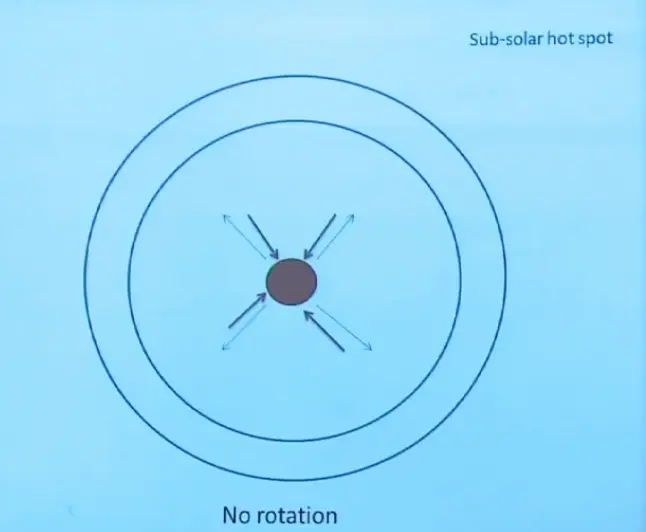
Let's look at the case when the planet is not rotating. So the point that's right under the Sun, if the Sun's down there, would heat up. And every other place, you'd get less and less sunlight. Whether you moved this way or that way, you'd get less and less sunlight, and you'd get no sunlight on the backside.

So you'd have a subsolar hot spot, just one very hot area right here. The low-level air would move in towards it. Those are the red arrows. And then, because the air gets heated, it would rise, and then aloft, it would spread out in all directions. And those are the thin blue arrows. So that's just like I built a bonfire here. You'd have air moving in towards it from all directions rising. And then when it hit the ceiling, it would go out in all directions.

Now, this is not at all what we have on Earth. This is the idealization or kind of a thought experiment of what the circulation would be if the Earth was not rotating on its axis. So don't take this as what happens. Take it as a building block to understand what actually happens in the Earth's atmosphere.

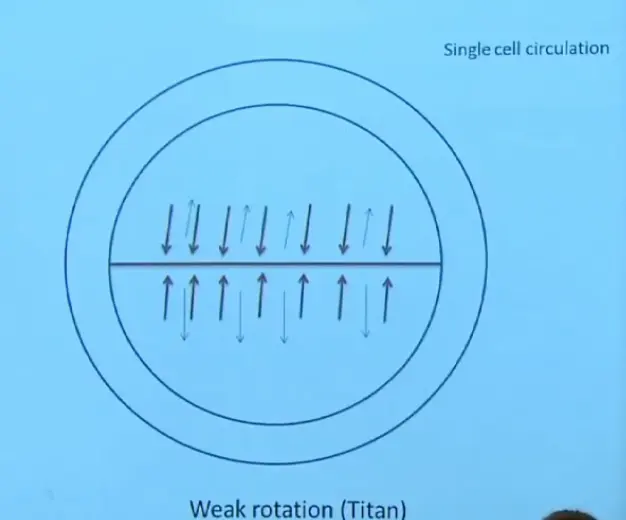
So let me bring in now the effect of distributing the heat zonally. So this would happen if I had weak rotation. I learned a few weeks ago in a lecture I went to on the planet Titan that actually the planet Titan fits into this kind of a description. It rotates rapidly enough to distribute the heat zonally but not so rapidly that the Coriolis force is a major player.

So here's what happens. You get a fairly uniform hot equator. Air moves towards it at low levels, gets heated, rises, and then moves away from it, poleward, at high elevations. It would sink somewhere out here and fall to the surface, and then move towards the hot line again, and then rise. You'd have a kind of planetary, simple bonfire kind of circulation towards and away from this heated line caused by the solar heat.

Effect of Earth’s Rotation: Circulation Cells [00:43:46]

For the Earth, we rotate somewhat faster than that. You know it takes 24 hours for us to have a day. That's a pretty fast rotation. By the way, this is sometimes called the single-cell circulation. Well, I guess there's two of them, but on one side of the equator, there's just one, rising, sinking, rising, sinking. So the single cell refers to what happens on either the northern or the southern hemisphere.

On Earth, you get something that's closer to a three-cell circulation, because the rotation rate is larger. So the Coriolis force is playing a larger role. You do get rising motion near the Equator, but it only goes slightly north and south and then sinks. And north of that, you get westerlies and then easterlies again, laid out like I have very crudely on this line diagram. I'm going to show you a better version of this in just a moment, but the main point is to show how much more complicated this is than that. And that all has to do with the stronger action of the Coriolis force.

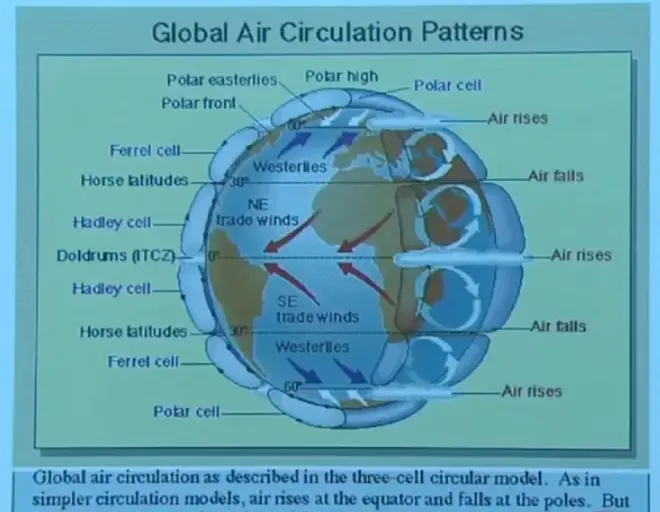
The rising motion along the Equator then gives you poleward-moving air aloft that descends at about 30 degrees north and south latitude. This is a very strong overturning cell. It's called the Hadley cell. And you must know about this one. This is really one of the dominant features of the climatology on Planet Earth is the Hadley cell.

Rising motion near the Equator, air moving poleward till it gets to about 30 degrees and then sinks, and then returns towards the Equator at the surface of the Earth. Because of the deflecting force from the Coriolis force, that air doesn't move directly towards the Equator. It comes in from the easterly direction. So it forms what we call the northeast trades, wind blowing from the northeast in the Northern Hemisphere, and the southeast trade winds in the Southern Hemisphere.

North and south of that, there is the Ferrel cell, which is a rather weak overturning in the opposite direction. But that's not the primary feature. I don't like this diagram, because they show the Ferrel cell so clearly, but they don't show the most obvious and dramatic feature of the westerlies, and that's the existence of these mid-latitude frontal cyclones. You won't see the Ferrel cell, but you'll see those mid-latitude frontal cyclones in that region.

And then in the polar regions, you get also a fairly weak cell giving you some easterly flow at the very high latitudes.

So this is the three-cell pattern of general circulation for Planet Earth. And I want to show you a set of satellite loops to try to illustrate a few of these features. This is a global view pieced together from a number of geostationary satellites posted at various longitudes around the globe. And it's looking at the emitted long-wave radiation. So we won't see day and night here. We're not counting on the Sun to illuminate these clouds. If we did that, it would go black, light, black, light as the Sun illuminated or not.

But instead, we're looking at the emitted radiation--Stefan-Boltzmann-type emitted radiation in the thermal infrared--and that'll tell us about where the clouds are and where the clear air is. For example, these light areas are clouds. They're higher, so they are colder. They emit less because they're higher. And that reduction in emission is shown here as a white region.

The lower parts and the surface of the ocean and the surface of the planet are hotter. They emit more. And that's illustrated here by a dark pixel. So you're basically looking at a moving temperature map of the Earth, where the temperature's mostly controlled by the height of the object that you're seeing. Some of the things you see here are the Intertropical Convergence Zone, where the trade winds are converging and the air is rising. And then your eye is really caught by these mid-latitude frontal cyclones. And?look at all these little comma-shaped cloud features here that represent this rapid flux of heat northwards and southwards, trying to balance the Earth's heat budget latitude by latitude.?