By: Tao Steven Zheng (鄭濤)

【Problem】

Hasan Ibn al-Haytham (Latinized: Alhazen, c. 965 – c. 1050) was an Arab scholar who studied mathematics, physics, astronomy, philosophy, and medicine. The “Lunes of Alhazen” originates from Al-Haytham’s attempt of squaring the circle. Let ?and ??be the area of the lunes (region shaded in blue and green), and? be the area of the right triangle (region shaded in red). Prove that the area of the two lunes is equal to the area of the right triangle.

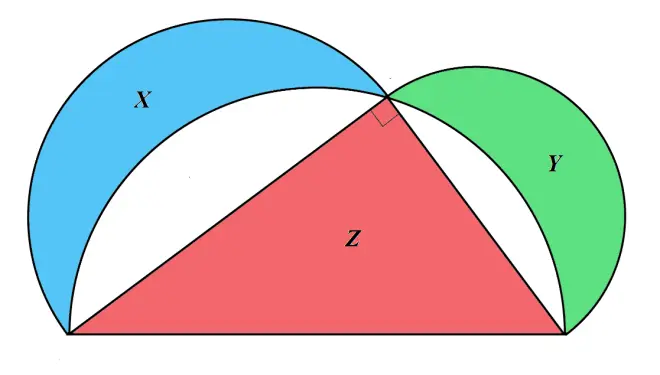
【Solution】

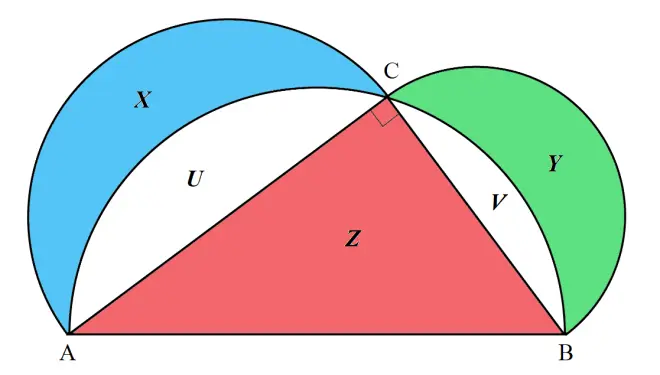
Let ?and ?be the area of the lunes (region shaded in blue and green), and? be the area of the right triangle (region shaded in red). Let? and be the area of the unshaded regions between the right triangles and the lunes.

The area of the right triangle is

The area of the unshaded regions (between the right triangle and the lunes) are equal to the area of the large semicircle of diameter? minus the area of the right triangle .

The area of the two lunes is equal to the sum of the areas of two semicircles (diameter and diameter ) minus the area of the unshaded regions.

?By the Pythagorean theorem,

Thus,

Therefore, the area of the two lunes is equal to the area of the right triangle!