By: Tao Steven Zheng (鄭濤)

【Problem】

?Jiuzhang Suanshu (Gougu 16)

Suppose there is a right triangle whose gou (shorter leg) is 8 bu, and gu (longer leg) is 15 bu. What is the diameter of the inscribed circle?

?

【Solution】

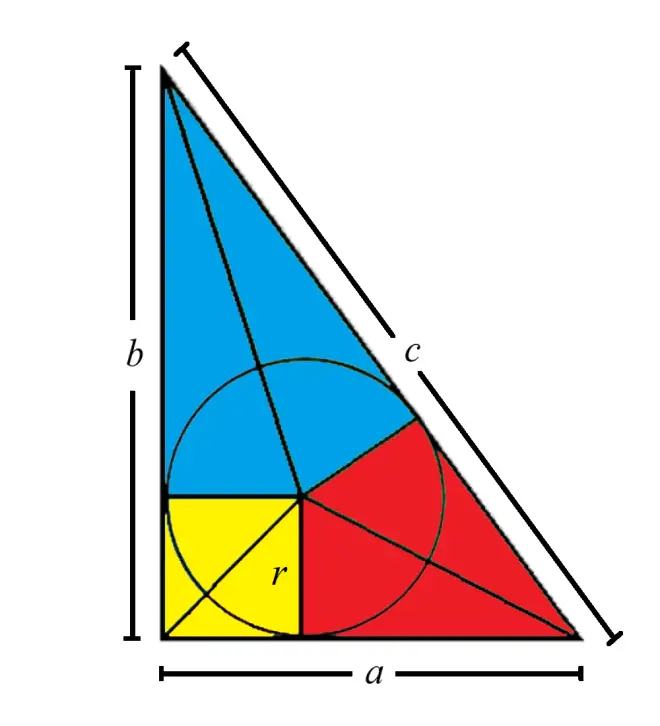
Let ?be the side lengths of the right triangle, where ?is the hypotenuse. Let ?be the radius and ?be the diameter of the inscribed circle. Dissect the right triangle into 6 pieces (Figure 1): 2 red triangles, 2 blue triangles, and 2 yellow triangles.

?

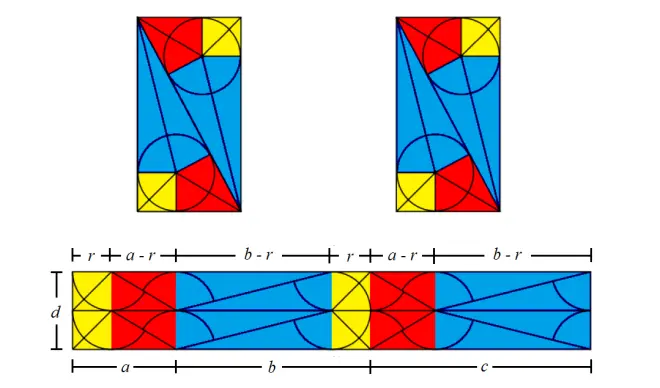
Copy each rectangle four times (Figure 2 top), then combine each pair of triangles of the same color to form rectangles (the yellow triangles form a square). Assemble them to form one large rectangle (Figure 2 bottom). Use this large rectangle to derive three different formulas for calculating the diameter of the inscribed circle.

Formula 1

The area of a large rectangle is equal to the area of four right triangles:

Formula 2

It can be seen immediately from (Figure 2 bottom) that:

It is known that and , thus

Formula 1

Formula 2

Therefore, the diameter of the inscribed circle is 6 bu.