ECON 159.?Game Theory

Lecture 02. Putting Yourselves into Other People's Shoes

https://oyc.yale.edu/economics/econ-159/lecture-2

We pointed out, that in this game, Alpha strictly dominates Beta. We mean that if these are your payoffs, no matter what your pair does, you attain a higher payoff from choosing Alpha, than you do from choosing Beta. Let's focus on a couple of lessons of the class before I come back to this. One lesson was, do not play a strictly dominated strategy. Everybody remember that lesson? Then much later on, when we looked at some more complicated payoffs and a more complicated game, we looked at a different lesson which was this: put yourself in others' shoes to try and figure out what they're going to do.?

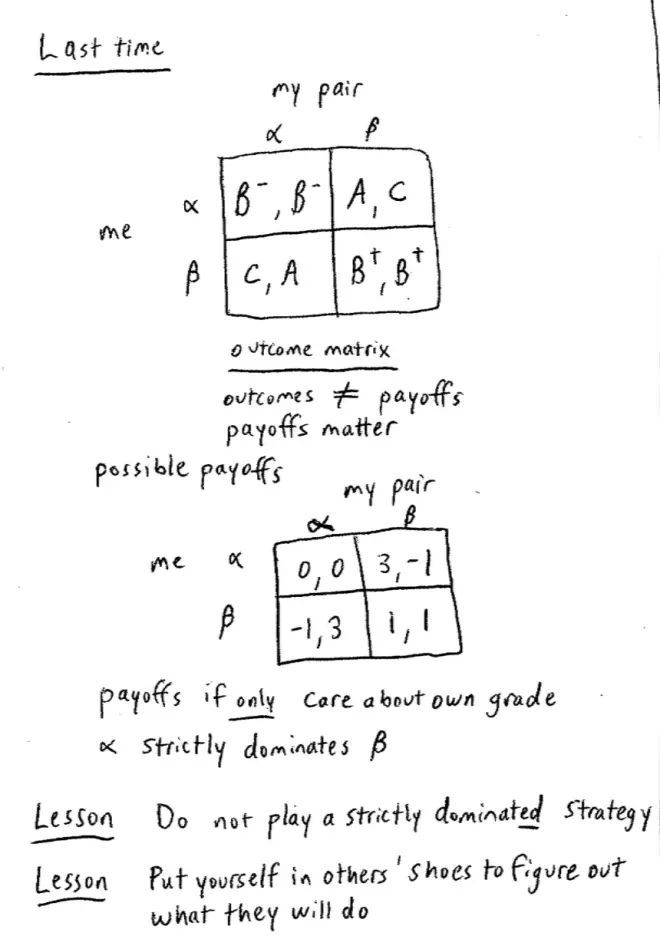
So in fact, what we learned from that is, it doesn't just matter what your payoffs are -- that's obviously important -- it's also important what other people's payoffs are, because you want to try and figure out what they're going to do and then respond appropriately.?

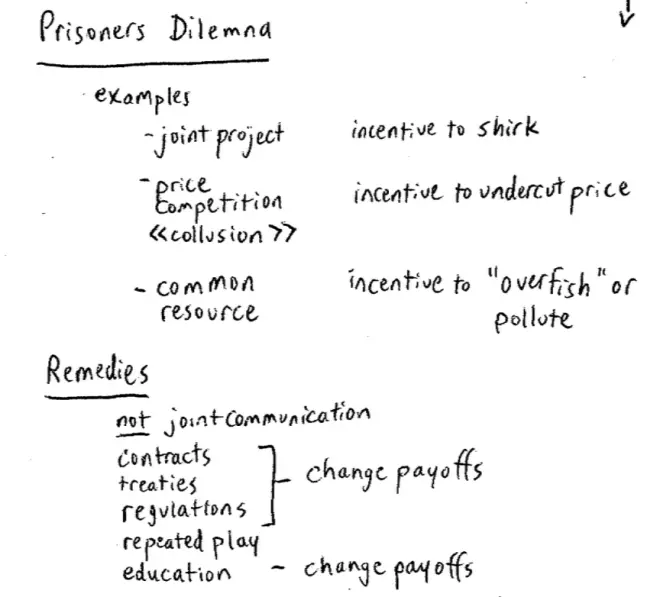
Again, still in the interest of recapping, this particular game is called the Prisoners' Dilemma.?Let me just reiterate and mention some more examples which are actually written here, so they'll find their way into your notes. So, for example, if you have a joint project that you're working on, perhaps it's a homework assignment, or perhaps it's a video project like these guys, that can turn into a Prisoners' Dilemma. Because each individual might have an incentive to shirk. Price competition -- two firms competing with one another in prices -- can have a Prisoners' Dilemma aspect about it.?Because no matter how the other firm, your competitor, prices you might have an incentive to undercut them. If both firms behave that way, prices will get driven down towards marginal cost and industry profits will suffer.?

Suppose there's a common resource out there, maybe it's a fish stock or maybe it's the atmosphere. There's a Prisoners' Dilemma aspect to this too. You might have an incentive to over fish. Because if the other countries with this fish stock--let's say the fish stock is the Atlantic--if the other countries are going to fish as normal, you may as well fish as normal too. And if the other countries aren't going to cut down on their fishing, then you want to catch the fish now, because there aren't going to be any there tomorrow.?

Another example of this would be global warming and carbon emissions. Again, leaving aside the science, about which I'm sure some of you know more than me here, the issue of carbon emissions is a Prisoners' Dilemma. Each of us individually has an incentive to emit carbons as usual. If everyone else is cutting down I don't have too, and if everyone else does cut down I don't have to, I end up using hot water and driving a big car and so on.?

We pointed out, that this is not just a failure of communication. Communication per se will not get you out of a Prisoners' Dilemma. You can talk about it as much as you like, but as long as you're going to go home and still drive your Hummer and have sixteen hot showers a day, we're still going to have high carbon emissions.?

You can talk about working hard on your joint problem sets, but as long as you go home and you don't work hard, it doesn't help. In fact, if the other person is working hard, or is cutting back on their carbon emissions, you have every bit more incentive to not work hard or to keep high carbon emissions yourself. So we need something more and the kind of things we can see more: we can think about contracts; we can think about treaties Between countries; we can think about regulation. All of these things work by changing the payoffs. Not just talking about it, but actually changing the outcomes actually and changing the payoffs, changing the incentives.?

Another thing we can do, a very important thing, is we can think about changing the game into a game of repeated interaction.?One last thing we can think of doing but we have to be a bit careful here, is we can think about changing the payoffs by education.

The formal parts of a game are this. We need players.?So the standard notation for players, I'm going to use things like little i and little j. So in that numbers game, the game when all of you wrote down a number and handed it in at the end of last time.?The players were you.

Second ingredient of the game are strategies.?So I'm going to use little "si" to be a particular strategy of Player i. So an example in that game might have been choosing the number 13. Now I need to distinguish this from the set of possible strategies of Player I, so I'm going to use capital "Si" to?be the set of alternatives. The set of possible strategies of Player i. So in that game we played at the end last time, what were the set of strategies? They were the sets 1, 2, 3, all the way up to 100.?

When distinguishing a particular strategy from the set of possible strategies. While we're here, our third notation for strategy, I'm going to use?little "s" without an "i," to mean a particular play of the game. So what do I mean by that? All of you, at the end last time, wrote down this number and handed them in so we had one number, one strategy choice for each person in the class. So here they are, here's my collected in, sort of strategy choices. Here's the bundle of bits of paper you handed in last time. This is a particular play of the game.?

I've got each person's name and I've got a number from each person: a strategy from each person. We actually have it on a spreadsheet as well: so here it is written out on a spreadsheet. Each of your names is on this spreadsheet and the number you chose. So that's a particular play of the game and that has a different name. We sometimes call this "a strategy profile." So in the textbook, you'll sometimes see the term a strategy profile or a strategy vector, or a strategy list. It doesn't really matter.?

So, to complete the game, we need payoffs. Again, I need notation for payoffs. So in this course, I'll try and use "U" for utile, to be Player i's payoff. So "Ui" will depend on Player 1's choice … all the way to Player i's own choice … all the way up to Player N's choices. So Player i's payoff "Ui," depends on all the choices in the class, in this case, including her own choice. Of course, a shorter way of writing that would be "Ui(s)," it depends on the profile.?

In the numbers game "Ui(s)" can be two things. It can be 5 dollars minus your error in pennies, if you won. I guess it could be something if there was a tie, I won't bother writing that now. And it's going to be 0 otherwise. So we've now got all of the ingredients of the game: players, strategies, payoffs.?

Now we're going to make an assumption today and for the next ten weeks or so; so for almost all the class. We're going to assume that these are known. We're going to assume that everybody knows the possible strategies everyone else could choose and everyone knows everyone else's payoffs. Now that's not a very realistic assumption and we are going to come back and challenge it at the end of semester, but this will be complicated enough to give us a lot of material in the next ten weeks.?

I'm going to write "s-i"?to mean a strategy choice for everybody except person "i". It's going to be useful to have that notation around. So this is a choice for all except person "i" or Player i. So, in particular, if you're person 1 and then "s-i" would be "s2, s3, s4" up to "sn" but it wouldn't include "s1." It's useful why? Because sometimes it's useful to think about the payoffs, as coming from "i's" own choice and everyone else's choices.?

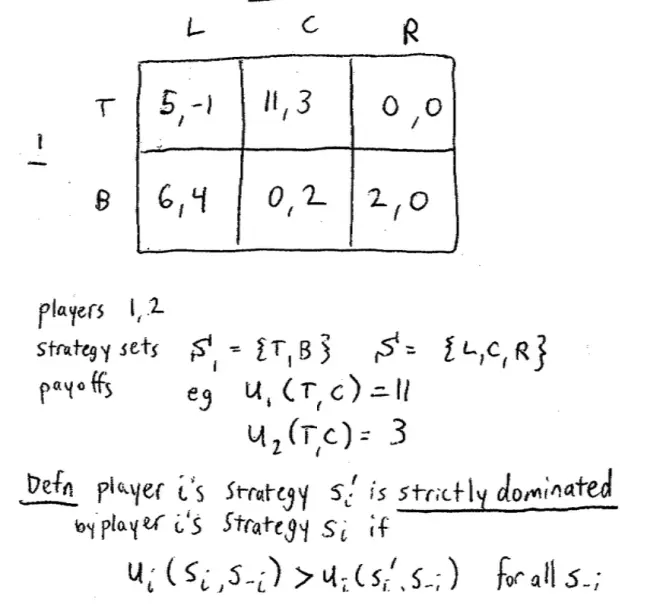
So let's have an example to help us fix some ideas.?It involves two players and we'll call the Players I and II and Player I has two choices, top and bottom, and Player II has three choices left, center, and right. It's just a very simple abstract example for now. And let's suppose the payoffs are like this. They're not particularly interesting. We're just going to do it for the purpose of illustration. So here are the payoffs: (5, -1), (11, 3), (0, 0), (6, 4), (0, 2), (2, 0).?

The players here in this game are Player I and Player II. What about the strategy sets or the strategy alternatives? So here Player I's strategy set, she has two choices top or bottom, represented by the rows, which are hopefully the top row and the bottom row. Player II has three choices, this game is not symmetric, so they have different number of choices.?Player II has three choices left, center, and right, represented by the left, center, and right column in the matrix.?

Just to point out in passing, up to now, we've been looking mostly at symmetric games. Notice this game is not symmetric in the payoffs or in the strategies. There's no particular reason why games have to be symmetric. So Player I's payoff, if she chooses top and Player II chooses center, we read by looking at the top row and the center column, and Player I's payoff is the first of these payoffs, so it's 11. Player II's payoff, from the same choices, top for Player I, center for Player II, again we go along the top row and the center column, but this time we choose Player II's payoff, which is the second payoff, so it's 3.?

Does Player I have a dominated strategy? No, Player I does not have a dominated strategy. Bottom is Better than top against left because 6 is bigger than 5, but top is Better than bottom against center because 11 is bigger than 0. So it's not the case that top always does Better than bottom, or that bottom always does Better than top.?

What about Player II? Does Player II have a dominated strategy??So in this particular game, I claim that center dominates right. If Player I chose top, center yields 3, right yields 0: 3 is bigger than 0. And if Player I chooses bottom, then center yields 2, right yields 0: 2 is bigger than 0 again. So in this game, center strictly dominates right. What you said was true, but I wanted something specifically about domination here. So what we know here, we know that Player II should not choose right.?

So definition : Player i's strategy "s'i" is strictly dominated by Player i's strategy "si," and now we can use our notation, if "UI" from choosing "si," when other people choose "s-i," is strictly bigger than UI(s'i) when other people choose "s-i," and the key part of the definition is, for all "s-i."?

So to say it in words, Player i's strategy "s'i" is strictly dominated by her strategy "si," if "si" always does strictly Better -- always yields a higher payoff for Player i -- no matter what the other people do.?

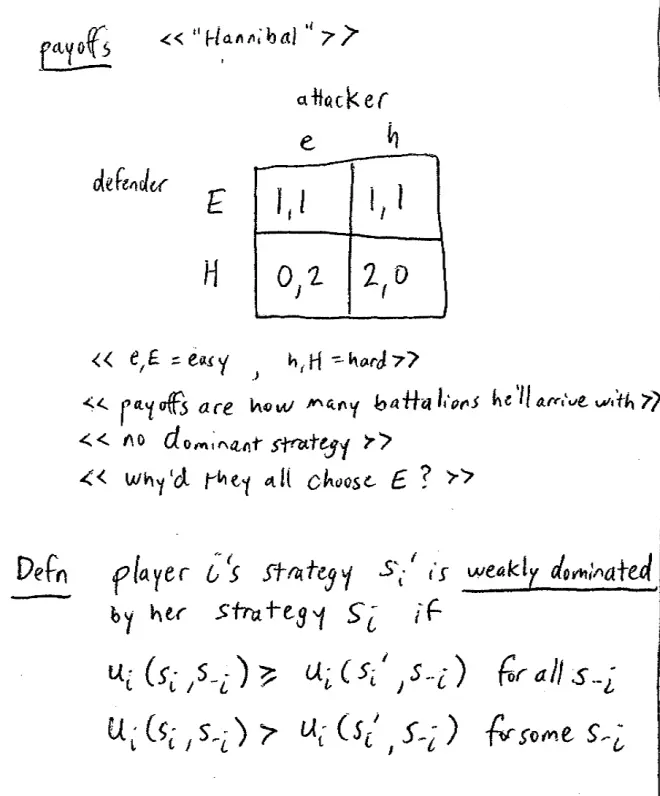
Let's have a look at another example. An invader is thinking about invading a country, and there are two ways through which he can lead his army. You are the defender of this country and you have to decide which of these passes or which of these routes into the country, you're going to choose to defend. And the catch is, you can only defend one of these two routes. The key here is going to be that there are two passes. One of these passes is a hard pass and the other one is an easy pass. It goes along the coast. If the invader chooses the hard pass he will lose one battalion of his army simply in getting over the mountains, simply in going through the hard pass. If he meets your army, whichever pass he chooses, if he meets your army defending a pass, then he'll lose another battalion.?

So the payoffs here are as follows, and I'll explain them in a second. So his payoff, the attacker's payoff, is how many battalions does he get to bring into your country.?He only has two to start with and for you, it's how many battalions of his get destroyed.?So just to give an example, if he goes through the hard pass and you defend the hard pass, he loses one of those battalions going over the mountains and the other one because he meets you. So he has none left and you've managed to destroy two of them. Conversely, if he goes on the hard pass and you defend the easy pass, he's going to lose one of those battalions. He'll have one left. He lost it in the mountains. But that's the only one he's going to lose because you were defending the wrong pass.?

Let's do the second lesson I emphasized at the beginning. Let's put ourselves in Hannibal's shoes, they're probably boots or something?and try and figure out what Hannibal's going to do here. So it could be--From Hannibal's point of view he doesn't know which pass you're going to defend, but let's have a look at his payoffs.?

We have to be a little bit careful. It's not the case that for Hannibal, choosing the easy pass to attack through, strictly dominates choosing the hard pass, but it is the case that there's a weak notion of domination here. It is the case -- to introduce some jargon -- it is the case that the easy pass for the attacker, weakly dominates the hard pass for the attacker. What do I mean by weakly dominate? It means by choosing the easy pass, he does at least as well, and sometimes Better, than he would have done had he chosen the hard pass.?

So here we have a second definition.?Definition- Player i's strategy, "s'i" is weakly dominated by her strategy "si" if Player i's payoff from choosing "si" against "s-i" is always as big as or equal, to her payoff from choosing "s'i" against "s-i" and this has to be true for all things that anyone else could do. And in addition, Player i's payoff from choosing "si" against "s-i" is strictly Better than her payoff from choosing "s'i" against "s-i," for at least one thing that everyone else could do.?

Just check, that exactly corresponds to the easy and hard thing we just had before. I'll say it again, Player i's strategy "s'i" is weakly dominated by her strategy "si" if she always does at least as well by choosing "si" than choosing "s'i" regardless of what everyone else does, and sometimes she does strictly Better. It seems a pretty powerful lesson. Just as we said you should never choose a strictly dominated strategy, you're probably never going to choose a weakly dominated strategy either, but it's a little more subtle.?

Now that definition, if you're worried about what I've written down here and you want to see it in words, on the handout I've already put on the web that has the summary of the first class, I included this definition in words as well. So compare the definition of words with what's written here in the nerdy notation on the board. Now since we think that Hannibal, the attacker, is not going to play a weakly dominated strategy, we think Hannibal is not going to choose the hard pass. He's going to attack on the easy pass. And given that, we should defend easy which is what most of you chose.?

So, by putting ourselves in Hannibal's shoes, we could figure out that his hard attack strategy was weakly dominated. He's going to choose easy, so we should defend easy. Having said that of course, Hannibal went through the mountains which kind of screws up the lesson, but too late now.?

"Without showing your neighbor what you are doing, put it in the box below a whole number Between 1 and a 100. We will (and in fact have) calculated the average number chosen in the class and the winner of this game is the person who gets closest to two-thirds times the average number. They will win five dollars minus the difference in pennies."

People in the room aren't going to choose at random.?On the whole, Yale students are not random number generators. They're trying to win the game. So they're unlikely to choose numbers at random. As a further argument, if in fact everyone thought that way, and if you figured out everyone was going to think that way, then you would expect everyone to choose a number like 33 and in that case you should choose a number like 22.?

So if you think people are going to play a particular way, in particular if you think people are going to?choose around 33, then 22 seems a great answer. But you underestimate your Yale colleagues. In fact, 22 was way too high. Now, again, let's just iterate the point here. Let me just repeat the point here. The point here is when you're playing a game, you want to think about what other people are trying to do, to try and predict what they're trying to do, and it's not necessarily a great starting point to assume that the people around you are random number generators.?

So, in particular, there's something about these strategy choices that are greater than 67 at any rate. Certainly, I mean 66 let's go up a little bit, so these numbers bigger than 67. What's wrong with numbers bigger than 67? So even if everyone in the room didn't choose randomly but they all chose a 100, a very unlikely circumstance, but even if everyone had chosen 100, the highest, the average, sorry, the highest two-thirds of the average could possibly be is 66 2/3, hence 67 would be a pretty good choice in that case.?

In particular, a strategy like 80 is dominated by choosing 67. You will always get a higher payoff from choosing 67, at least as high and sometimes higher, than the payoff you would have got, had you chosen 80, no matter what else happened in the room. So these strategies are dominated. We know, from the very first lesson of the class last time, that no one should choose these strategies. They're dominated strategies.?

We know no one's going to choose 68 and above, so we can just forget them. We can delete those strategies and once we delete those strategies, all that's left are choices 1 through 67. Once we've figured out that no one should choose a strategy bigger than 67, then we can go another step and say, if those strategies never existed, then the same argument rules out?strategies bigger than 45. Let's be careful here. The strategies that are less than 67 but bigger than 45, I think these strategies are not, they're not dominated strategies in the original game. In particular, we just argued that if everyone in the room chose a 100, then 67 would be a winning strategy. So it's not the case that the strategies Between 45 and 67 are dominated strategies. But it is the case that they're dominated once we delete the dominated strategies: once we delete 67 and above.?

So these strategies -- let's be careful here with the word weakly here -- these strategies are not weakly dominated in the original game. But they are dominated -- they're weakly dominated -- once we delete 68 through 100. So all of the strategies 45 through 67, are gone now.?

So without writing that argument down in detail, notice that we can rule out the strategies 30 through 45, not by just examining our own payoffs; not just by putting ourselves in other people's shoes and realizing they're not going to choose a dominated strategy; but by putting our self in other people's shoes while they're putting themselves in someone else's shoes and figuring out what they're going to do. So this is an 'in shoes', be careful where we are here, this is an 'in shoes in shoes' argument, at which point you might want to invent the sock.?Where's this argument going to go? It's going to go all the way down to 1: all the way down to 1.?

I want to discuss the consequence of rationality in playing games, slightly philosophical for a few minutes. So I claim that if you are a rational player, by which I mean somebody who is trying to maximize their payoffs by their play of the game, that simply being rational, just being a rational player, rules out playing these dominated strategies.

It's not necessarily that the four people who chose Between 46 and 67 are themselves "thick," it's that they think the rest of you are "thick." Down here, this doesn't require people to be thick, or to think the rest of you are thick, they're just people who think that you think?they're just people who think that you think that they're thick and so on. But again, all the way to 1 we're going to need very, very many rounds of knowledge?of rationality.?

Does anyone know what we call it if we assume an infinite sequence of "I know that you know that I know that you know that I know that you know that I know that you know" something? What's the expression for that??The technical expression of that in philosophy is common knowledge. Common knowledge is: "I know something, you know it, you know that I know it, I know that you know it, I know that you know that I know it, etc., etc. etc.: an infinite sequence.?

But if we had common knowledge of rationality in this class, then the optimal choice would have been 1. Okay, so why was it that 1 wasn't the winning answer? Why wasn't 1 the winning answer? So to get all the way to 1, we need a lot. We need not just that you're all rational players, not just that you know each other's rational, but you know everyone else's rational. I mean I know you all know each other because you've met at Yale, but you also know each other well enough to know that not everyone in the room is rational, and you're pretty sure that not everyone knows that you're rational and so on and so forth. It's asking a lot to get to 1 here, and in fact, we didn't get to 1.?

What is it about talking about this game that makes a difference? Let me hazard a guess here. I think what makes a difference is not only do you, yourselves, know Better how to play this game now, but you also know that everybody around you knows Better how to play the game. Discussing this game raised not just each person's sophistication, but it raised what you know about other people's sophistication, and you know that other people now know that you understand how to play the game.?

So the main lesson I want you to get from this is that not only did it matter that you need to put yourself in other people's shoes and think about what their payoffs are. You also need to put yourself into other people's shoes and think about how sophisticated are they at playing games. And you need to think about how sophisticated do they think you are at playing games. And you need to think about how sophisticated do they think that you think that they are at playing games and so on. This level of knowledge, these layers of knowledge, lead to very different play in the game. And to make this more concrete, if a firm is competing against a competitor it can be pretty sure, that competitor is a pretty sophisticated game player and knows that the firm is itself. If a firm is competing against a customer -- let's say for a non-prime loan -- perhaps that assumption is not quite so safe. It matters in how we take games through to the real world, and we're going to see more of this as the term progresses.?

What is known here? Well I'll reveal the facts now: that in fact Ale knows that Kaj has a pink hat on his head. So it's true that Ale knows that at least one person in the room has a pink hat on their head. And it's true that Kaj knows that Ale has a pink hat on his head. They both look absurd, but never mind. But notice that Ale doesn't know the color of the hat on his own head. So even though both people know, even though it is mutual knowledge that there's at least one pink hat in the room, Ale doesn't know what Kaj is seeing. So Ale does not know that Kaj knows that there's a pink hat in the room. In fact, from Ale's point of view, this could be a blue hat. So again, they both know that someone in the room has a pink hat on their head: it is mutual knowledge that there's a pink hat in the room. But Ale does not know that Kaj knows that he is wearing a blue, a pink hat, and Kaj does not know that Ale knows that Kaj is wearing a pink hat. Each of their hats -- each of their own hats -- might be blue.?

?Common knowledge is a subtle thing. Mutual knowledge doesn't imply common knowledge. Common knowledge is a statement about not just what I know. It's about what do I know the other person knows that I know that the other person …and so on and so forth. Even in this simple example, while you might think it's obviously common knowledge, it wasn't common knowledge that there was a pink hat in the room.