散文網(wǎng) » 科技 »學(xué)習(xí) » [Number Theory] Square Root of the Primes

[Number Theory] Square Root of the Primes

2021-10-12 16:14 作者:AoiSTZ23 0人讀過(guò) | 我要投稿

By: Tao Steven Zheng (鄭濤)

【Problem】

A prime number is a natural number greater than 1 that has no positive integer divisors other than 1 and itself.

An irrational number is a number that cannot be expressed as a fraction $%5Cfrac%7Bm%7D%7Bn%7D$ for any integers $m$ and $n$ .

Prove that the square root of a prime number is an irrational number.

【Solution】

Let $p$ be a prime number. If $%5Csqrt%7Bp%7D$ to be rational, it must be expressible as the quotient of two coprime integers, say $m%2C%20n%20$ , where $gcd(m%2Cn)%20%3D%201$ .

$%20%5Csqrt%7Bp%7D%20%3D%20%5Cfrac%7Bm%7D%7Bn%7D$

Squaring both sides of the equation, we get

$p%20%3D%20%5Cfrac%7Bm%5E2%7D%7Bn%5E2%7D$

$pn%5E2%20%3D%20m%5E2$

Express $m$ and $n$ as the product of powers of unique prime factors:

$m%20%3D%20%7Bp%7D_%7B1%7D%5E%7B%7B%5Calpha%7D_%7B1%7D%7D%20%7Bp%7D_%7B2%7D%5E%7B%7B%5Calpha%7D_%7B2%7D%7D%20%7Bp%7D_%7B3%7D%5E%7B%7B%5Calpha%7D_%7B3%7D%7D%20...%20%7Bp%7D_%7Bi%7D%5E%7B%7B%5Calpha%7D_%7Bi%7D%7D$

$n%20%3D%20%7Bq%7D_%7B1%7D%5E%7B%7B%5Cbeta%7D_%7B1%7D%7D%20%7Bq%7D_%7B2%7D%5E%7B%7B%5Cbeta%7D_%7B2%7D%7D%20%7Bq%7D_%7B3%7D%5E%7B%7B%5Cbeta%7D_%7B3%7D%7D%20...%20%7Bq%7D_%7Bj%7D%5E%7B%7B%5Cbeta%7D_%7Bj%7D%7D$

Thus, $pn%5E2%20%3D%20m%5E2$ becomes

$p%7B%5Cleft(%7Bq%7D_%7B1%7D%5E%7B%7B%5Cbeta%7D_%7B1%7D%7D%20%7Bq%7D_%7B2%7D%5E%7B%7B%5Cbeta%7D_%7B2%7D%7D%20%7Bq%7D_%7B3%7D%5E%7B%7B%5Cbeta%7D_%7B3%7D%7D%20...%20%7Bq%7D_%7Bj%7D%5E%7B%7B%5Cbeta%7D_%7Bj%7D%7D%5Cright)%7D%5E%7B2%7D%20%3D%20%7B%5Cleft(%7Bp%7D_%7B1%7D%5E%7B%7B%5Calpha%7D_%7B1%7D%7D%20%7Bp%7D_%7B2%7D%5E%7B%7B%5Calpha%7D_%7B2%7D%7D%20%7Bp%7D_%7B3%7D%5E%7B%7B%5Calpha%7D_%7B3%7D%7D%20...%20%7Bp%7D_%7Bi%7D%5E%7B%7B%5Calpha%7D_%7Bi%7D%7D%20%5Cright)%7D%5E%7B2%7D%20$

$p%5Cleft(%7Bq%7D_%7B1%7D%5E%7B2%7B%5Cbeta%7D_%7B1%7D%7D%20%7Bq%7D_%7B2%7D%5E%7B2%7B%5Cbeta%7D_%7B2%7D%7D%20%7Bq%7D_%7B3%7D%5E%7B2%7B%5Cbeta%7D_%7B3%7D%7D%20...%20%7Bq%7D_%7Bj%7D%5E%7B2%7B%5Cbeta%7D_%7Bj%7D%7D%5Cright)%20%3D%20%5Cleft(%7Bp%7D_%7B1%7D%5E%7B2%7B%5Calpha%7D_%7B1%7D%7D%20%7Bp%7D_%7B2%7D%5E%7B2%7B%5Calpha%7D_%7B2%7D%7D%20%7Bp%7D_%7B3%7D%5E%7B2%7B%5Calpha%7D_%7B3%7D%7D%20...%20%7Bp%7D_%7Bi%7D%5E%7B2%7B%5Calpha%7D_%7Bi%7D%7D%20%5Cright)$

According to the right hand side of the equation, the exponents of all unique prime factors all become even numbers (any integer multiplied by 2 is an even number). This suggests that if the two sides are to equate, the left hand side of the equation should also be comprised of unique prime factors with even powers. However, there is an extra factor $p$ that makes this impossible. There are two cases to show: one, if $p$ occur in the prime factorization of $m%5E2$ ; two, if $p$ does not occur in the prime factorization of $m%5E2$ .

Case 1: If $p$ does occur in the prime factorization of $m%5E2$ , then, say $p%20%3D%20q_j$ , we get a factor $p%5Cleft(q_%7Bj%7D%5E%7B2%7B%5Cbeta%7D_%7Bj%7D%7D%20%5Cright)%20%3D%20%7Bp%7D%5E%20%7B2%7B%5Cbeta%7D_%7Bj%7D%20%2B%201%7D$ , which is a prime factor with an odd power. This contradicts our above assumption that the left hand side of the equation must contain only prime factors with even powers.

Case 2: If $p$ does not occur in the prime factorization of $m%5E2%20$ , then we get a unique prime factor $p$ with an odd power (1). Once again, this contradicts our above assumption that the left hand side of the equation must contain only prime factors with even powers.

Since the above two cases are clear contradictions, we must reject the assumption that $%5Csqrt%7Bp%7D$ is rational. Therefore, the square root of a prime number is irrational.

【Historical Note】

Hippasus of Metapontum (fl. 500 BC) was a philosopher and early follower of Pythagoras who first proved (a much simpler proof) that the square root of 2 is irrational. Some traditions say that he was drowned after revealing this mathematical truth!

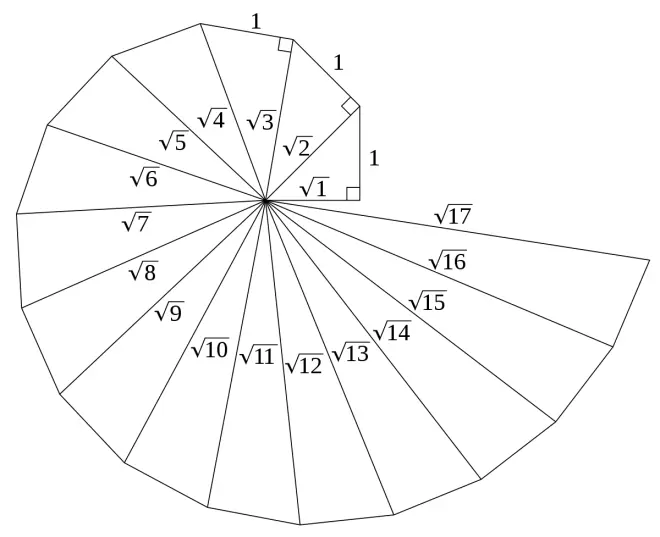
The above diagram is called the Spiral of Theodorus, attributed to Theodorus of Cyrene (c. 465 - 399 BC) by the Greek philosopher Plato. Theodorus proved that the square root of non-square integers are irrational between 1 and 17. Our proof is only focused on the prime numbers, so extends to infinity (Euclid proved there are infinitely many primes).

標(biāo)簽：