ECON 159.?Game Theory

Lecture?05. Nash Equilibrium: Bad Fashion and Bank Runs

https://oyc.yale.edu/economics/econ-159/lecture-5

Let's start by putting down a formal definition. A strategy profile--remember a profile is one strategy for each player, so it's going to be S1*, S2*, all the way up to SM* if there are M players playing the game--so this profile is a Nash Equilibrium?if, for each i –so for each player i, her choice--so her choice here is Si*, i is part of that profile is a best response to the other players' choices. Of course, the other players' choices here are S--i* so everyone is playing a best response to everyone else.?

It's not always going to be the case that people always play a Nash Equilibrium. For example, when we played the numbers game, the game when you chose a number,?the equilibrium in that game is for everyone to choose one, but when we actually played the game, the average was much higher than that: the average was about 13. It is true that when we played it repeatedly, it seemed to converge towards 1, but the play of the game when we played it just one shot first time, wasn't a Nash Equilibrium. So we shouldn't form the mistake of thinking people always play Nash Equilibrium or people, "if they're rational," play Nash Equilibrium. Neither of those statements are true.?

Nevertheless, there are some good reasons for thinking about Nash Equilibrium other than the fact it's used by other people.?So I want to put down some motivations here--the first motivation is the idea of "no regrets." So what is this idea? It says, suppose we're looking at a Nash Equilibrium. If we hold the strategies of everyone else fixed, no individual i has an incentive to deviate, to move away. Holding everyone else's actions fixed, no individual has any incentive to move away. Let me be a little more careful here; no individual has any?strict?incentive to move away. No individual can do strictly better by deviating, holding everyone else's actions.

A second idea is that a Nash Equilibrium can be thought of as self-fulfilling beliefs.?If everyone in the game believes that everyone else is going to play their part of a particular Nash Equilibrium then everyone, will in fact, play their part of that Nash Equilibrium. Why is it the case if everyone believes that everyone else is playing their part of this particular Nash Equilibrium that that's so fulfilling and people actually will play that way??

It's almost a repeat of the first thing. If I think everyone else is going to play their particular--if I think players 2 through N are going to play S2* through SN*--then by definition my best response is to play S1* so I will in fact play my part in the Nash Equilibrium.

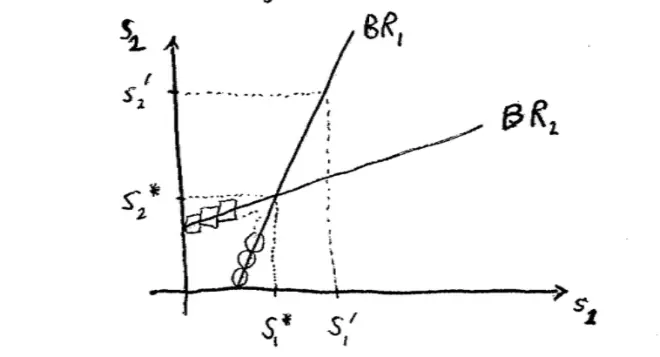
So, we had this picture last time in the partnership game in which people were choosing effort levels. And this line was the best response for Player 1 as a function of Player 2's choice. And this line was the best response of Player 2 as a function of Player 1's choice. The Nash Equilibrium is where the lines cross.

So, how about self-fulfilling beliefs? If Player 1 believes that Player 2 is going to choose this strategy, then Player 1 should choose this strategy,?that's what it means to be best response. But if Player 1 thinks that Player 2 is playing exactly her Nash strategy then Player 1's best response is to respond by playing his Nash strategy. And conversely, if Player 2 thinks Player 1 is playing his Nash strategy, then Player 2's best response indeed is to play her Nash strategy. So, you can that's a self-fulfilling belief. If both people think that's what's going to happen, that is indeed what's going to happen.?

How about the idea of no regrets? So here's Player 1; he wakes up the next morning and he says, "I chose S1*, do I regret this?" Well, now he knows what Player 2 chose; Player 2 chose S2* and he says, "no that's the best I could have done. Given that Player 2 did in fact choose S2*, I have no regrets about choosing S1*.?So, only at the Nash Equilibrium are there no regrets.?

So, I want to spend quite a lot of time today just getting used to the idea of Nash Equilibrium and trying to find Nash Equilibrium.?

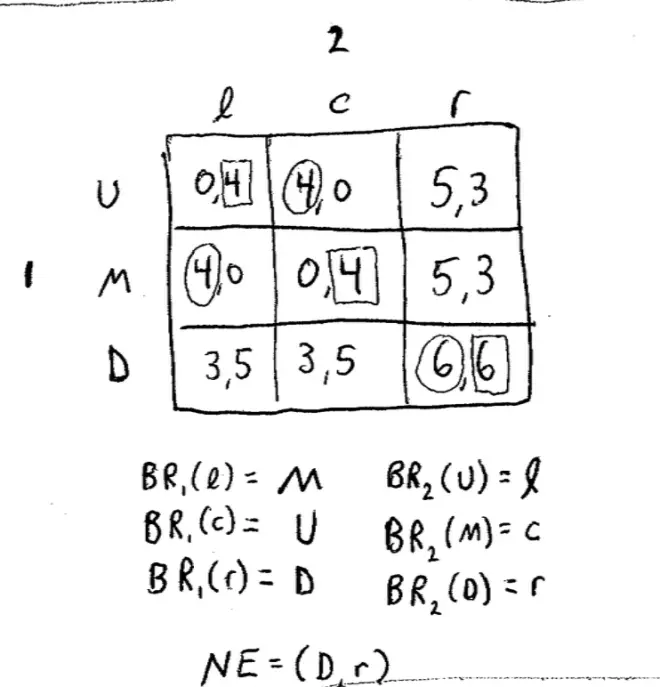
Let's start with this game, very simple game with two players. Each player has three strategies and I'm not going to motivate this game. Player 1 can choose up, middle, or down, and Player 2 can choose left, center, and right and the payoffs are as follows: (0,4) (4,0) (5,3) (4,0) (0,4) (5,3) again (3,5) (3,5) and (6,6).?The way we're going to go about finding them is going to?figure?out Player 1's best responses and Player?2's best responses: Player 1's best response to what Player 2's doing and Player 2's best response to what Player 1 is doing; and then we looked where they coincided and that was the Nash Equilibrium.?

Player 1's best response in this case is middle, because 4 is bigger than 0, and it's bigger than 3. What is the?Player 1's best response if Player 2 chooses center? Up is the correct answer.?Just as the Nash Equilibrium must be where these best response lines coincided here because that's the point at which each player is playing a best response to each other, so the Nash Equilibrium over here is?the down-right square.?

Nash Equilibrium goes a little further in narrowing down our predictions. But we also learned something from that. We argued last time, in the last few weeks, that rationality, or even mutual knowledge of rationality or even common knowledge of rationality couldn't really get us much further than deleting dominated strategies, or if you like, deleting strategies that are never best responses. Rationality, and those kinds of arguments should not lead us to the conclusion that people necessarily play Nash Equilibrium.?

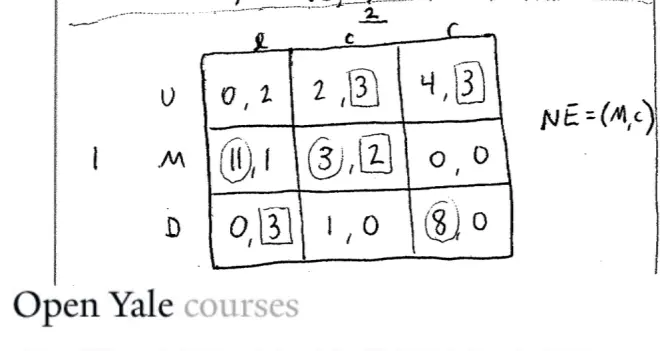
Let's have a look at another example. Again, we'll keep it simple for now and we'll keep to a two-player, three-strategy game; up, middle, down, left, center, right and this time the payoffs are as follows: (0,2) (2,3) (4,3) (11,1) (3,2) (0,0) (0,3) (1,0) and (8,0). Notice that the middle of center?is a Nash Equilibrium. Why is it the Nash Equilibrium? Because each player is playing a best response to each other. If I'm Player 1 and I think that Player?2 is playing center, I should play middle. If I'm Player 2, I think Player 1 is playing middle, I should play center. If, in fact, we play this way neither person has any regrets. Notice they didn't do particularly well in this game. In particular, Player?1 would have liked to get this 11 and this 8, but they don't regret their action because, given that Player 2 played center, the best they could have got was 3, which they got by playing middle. Notice in passing in this game, that best responses needn't be unique. Sometimes they can be a tie in your best response. It could happen.?

Let's go back earlier in the course, and ask how does it relate to the idea of dominance? This will be our third concept in this course. We had a concept about dominance, we had a concept about best response, and now we're at Nash Equilibrium. It's, I think, obvious how it relates to best response: it's when best responses coincide. How about how it relates to dominance? What we're going to do is we're going to relate the Nash Equilibrium to our idea of dominance, or of domination, and to do that an obvious place to start is to go back to a game that we've seen before.?

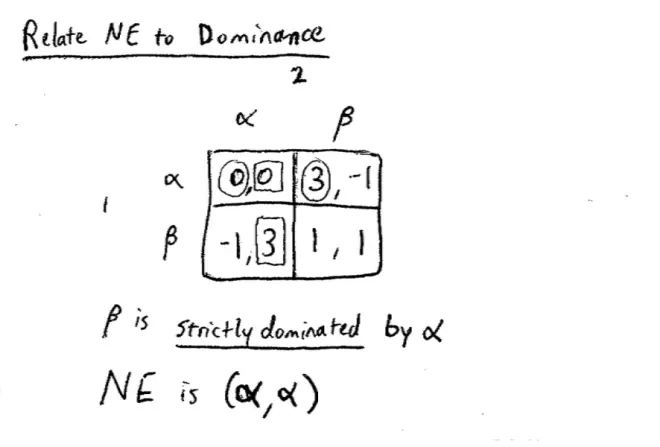
So here's a game where Player 1 and Player 2 are choosing ? and β and the payoffs are (0,0) (3,-1) (-1,3) and (1,1).?This is the Prisoner's Dilemma. We know in this game that β is is strictly dominated by ?.

So now, let's find the Nash Equilibrium in this game. So, the best response to ? must be ?. The best response to β must be ?, and for the column player the best response to ? must be ?, and the best response to β must be ?. So?the Nash Equilibrium in this game is (?, ?). In other words, it's what we would have arrived at had we just deleted strictly dominated strategies. So, here's a case where ? strictly dominates β, and sure enough Nash Equilibrium coincides, it gives us the same answer, both people choose ? in this game.?

I'm going to claim it's the case, that no strictly dominated strategy--in this case β--no strictly dominated strategy could ever be played in a Nash Equilibrium. A?strictly dominated strategy is never a best response to anything. In particular, the thing that dominates it always does better. So, in particular, it can't be a best response to the thing being played in the Nash Equilibrium. So that's actually a very good proof that proves that no strictly dominated strategy could ever be played in a Nash Equilibrium.?

But now we have, unfortunately, a little wrinkle, and the wrinkle, unfortunately, is weakly dominated--is weak domination. So we've argued, it was fairly easy to argue, that no strictly dominated strategy is ever going to reappear annoyingly in a Nash Equilibrium. But unfortunately, the same is not true about weakly dominated strategies. Deleting weakly dominated strategies can lead you to do things that might make you feel a little bit uneasy. So weak domination is really not such a secure notion as strict domination, and we'll see here as a trivial example of that.?

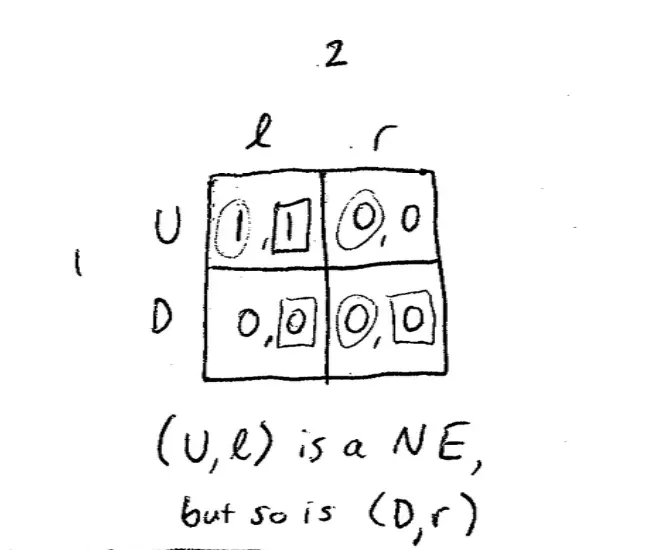
And again, so here's the trivial example, not an interesting example, but it just makes the point. So here's a 2 x 2 game. Player 1 can choose up or down and Player 2 can choose left or right, and the payoffs are really trivial: (1,1) (0,0) (0,0) (0,0). So the best response for Player 1, if Player?2 plays left is clear to choose up. And the best response of Player 1 if Player 2 chooses right is--well, either up or down will do, because either way he gets 0. So these are both best responses.?

Conversely, Player 2's best response if Player 1 chooses up is, sure enough, to choose left, and that's kind of the answer we'd like to have, but unfortunately, when Player 1 plays down, Player 2's best response is either left or right. It makes no difference. They get 0 either way.?

Notice the first observation is that there's more than one Nash Equilibrium in this game. ?It's hard to imagine coming up with an argument that wouldn't lead you to choose up and left in this game.?Up left is a Nash Equilibrium but so is down right. If Player 2 is choosing right, your best response weakly is to choose down. If Player?1 is choosing down, Player 2's best response weakly is to choose right. Here, this is arriving because of the definition of Nash; it's a very definite definition.?

When we looked at the definition we said, something is a Nash Equilibrium was each person is playing a best response to each other; another way of saying that is no player has a strict incentive to deviate. No player can do strictly better by moving away. So here at down right Player 1 doesn't do strictly better; it's just a tie if she moves away. And Player 2 doesn't do strictly better if he moves away. It's a tie. He gets 0 either way.?

In this case one of the Nash Equilibria seems silly.?It's obvious in some sense that the upper-left?has to be the sensible prediction. So, just a sort of worrying note before we move on. So, this was pretty formal and kind of not very exciting so far, so let's try and move on to something a little bit more fun.?

So, what I want to do now is I want to look at a different game.?I want to convince you how to find--to discuss how to find Nash Equilibria in the game which, unlike these games, doesn't just have two players--it has many players--but fortunately, not many strategies per player.?

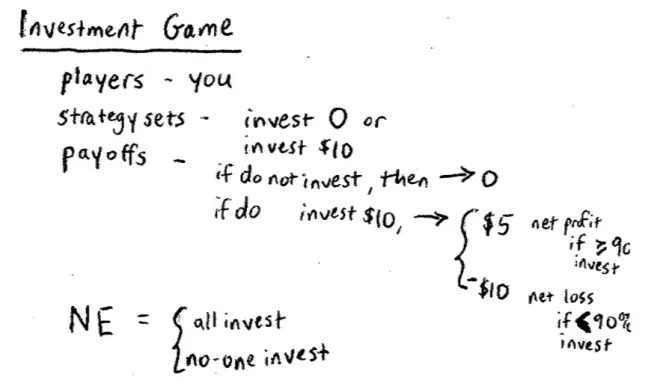
So this is going to be called The Investment Game.?The strategies in this game are very simple, the strategy sets, or the strategy alternatives. Each of you can choose between investing nothing in a class project, $0, or invest $10. So, I'm sometimes going to refer to investing nothing as not investing. You're either going to invest $10 or nothing, you're not going to invest. What we're missing are the payoffs.?

So here are the payoffs; so the payoffs are as follows: if you do not invest, you invest nothing, then your payoff is $0. So nothing ventured nothing gained: natural thing. But if you do invest $10, remember each of you is going to invest $10 then your individual payoffs are as follows.?You're going to get a profit of $5. The way this is going to work is you're going to invest $10 so you'll make a gross profit of $15 minus the $10 you originally invested for a net of $5.?But that requires more than 90% of the class to invest, greater than or equal to 90% of the class to invest. If more than 90% of the class invests, you're going to make essentially 50% profit.?

Unfortunately, the bad news is you're going to lose your $10, get nothing back so this is a net loss, if fewer than 90% of the class invest. I mean a key rule here; you're not allowed to talk to each other: no communication in the class. No hand signals, no secret winks, nothing else.

Don't look around; just raise your hands, everyone who invested? Everyone who didn't invest! Oh that's more than 10%. Let's do that again. So everyone who invested raised their hands … and everyone who didn't invest raise their hands. So I don't know what that is, maybe that's about half. So now I'm thinking we should have played this game for real. I want to get some discussion going about this.

We have lots of different views out here. We have half the people investing and half the people not investing roughly, and I think you can make arguments either way. So we'll come back to whether it's exactly the same as the game we just saw.?

There are two Nash Equilibria here, one is all invest and another one is no one invest. These are both Nash Equilibria in this game. And let's just check that they are exactly the argument that Kate said. That if everyone invests then no one would have any regrets, everyone's best response would be to invest. If nobody invests, then everyone would be happy not to have invested, that would be a best response.?

It?is a game with two equilibria like the previous game and there were other similarities to the previous game, but it's a little bit--the equilibria in this case are not quite the same as the other game. In the other game that other equilibrium, the (0,0) equilibrium seemed like a silly equilibrium. It isn't like we'd ever predict it happening.?Whereas here, the equilibrium with nobody investing actually is quite a plausible equilibrium. If I think no one else is investing then I strictly prefer not to invest.

In principle, you could have looked at every possible combination and there's lots of possible combinations. It could have been a combination where 1% invested and 99% didn't, and 2% invested and 98% didn't and so on and so forth.?

Both of you are being more rigorous and more mathematical than I'm tempted to be here. I think the easy method here--the easy sophisticated math here is "to guess." My guess is the easy thing to do is to guess what flight would be the equilibrium here and then what? Then check; so a good method here in these games is to guess and check. And guess and check is really not a bad way to try and find Nash Equilibria. The reason it's not a bad way is because checking is fairly easy. Guessing is hard but?checking with something that you--some putative equilibrium, some candid equilibrium, checking whether it is an equilibrium is easy because all you have to do is check that nobody wants to move, nobody wants to deviate. So again, in practice that's what you're going to end up doing in this game, and it turns out to be very easy to guess and check, which is why you're able to find it. So guess and check is a very useful method in these games where there are lots and lots of players, but not many strategies per player, and it works pretty well.?

Let's do it again, second time,?third time, hang on a second.?Now, if you invested the third time raise your hand. Where are we heading here? Where are we heading pretty rapidly? We're heading towards an equilibrium; let's just make sure we confirm that. There are certain circumstances in which play converges in the natural sense--not in a formal sense but in a natural sense--to an equilibrium. With the exception of a few dogged people who want to pay for my lunch, almost everyone else was converging to an equilibrium. So play converged fairly rapidly to the Nash Equilibrium.?

But we discussed there were two Nash Equilibria in this game. Is one of these Nash Equilibria better than the other??Everyone investing is a better Nash Equilibrium for everyone in the class, than everyone not investing, is that correct? Nevertheless, where we were converging in this case was what? Where we're converging was the bad equilibrium. We were converging rapidly to a very bad equilibrium, an equilibrium which no one gets anything, which all that money is left on the table.?

So how can that be? How did we converge to this bad equilibrium? To be a bit more formal, the bad equilibrium and no invest equilibrium here, is?pareto?dominated by the good equilibrium. Everybody is strictly better off at the good equilibrium than the bad equilibrium. It?pareto?dominates, to use an expression you probably learned in 150 or 115. Nevertheless, we're going to the bad one; we're heading to the bad equilibrium.?

Why did we end up going to the bad equilibrium rather than the good equilibrium??Suppose the first time we played the game in this class this morning, suppose that 93% of the class had invested. In which case, those 93% would all have made money. My guess is, we might have converged the other way and converged up to the good equilibrium. Does that make sense? So people figured out that they--people who didn't invest the first time--actually they played the best response to the class, so they stayed put. And those of you did invest, a lot of you started not investing as you caught up in this spiral downward and we ended up not investing.?

But had we started off above the critical threshold, the threshold here is 90%, and had you made money the first time around, then it would have been the non-investors that would have regretted that choice and they might have switched into investing, and we might have--I'm not saying necessarily, but we might have gone the other way.

Notice that what happened here, the way we spiraled down coincides with something we've talked about Nash Equilibrium already, it coincides with this idea of a self-fulfilling prediction. Provided you think other people are not going to invest, you're not going to invest. So, it's a self-fulfilling prediction to take you down to not investing. Conversely, provided everyone thinks everyone else is going to invest, then you're going to go up to the good equilibrium. If it was a bare market, it looked like everyone else didn't have confidence in everyone else investing, and then that was a self-fulfilling prophesy and we ended up with no investment.?

In Prisoner's Dilemma playing ? was always a best response. What led us to the bad outcome in Prisoner's Dilemma was that ?, the defense strategy, the non-cooperative strategy, the not helping tidy your room strategy, was always the best thing to do. Here, in some sense the "good thing," the "moral thing" in some sense, is to invest but it's not the case that not investing dominates investing. In fact, if all the people invest in the room you ought to invest, is that right? So this is a social problem, but it's not a social problem of the form of a Prisoner's Dilemma.

This is a coordination game. Because you'd like everyone in the class to coordinate their responses on invest. In fact, if they did that, they all would be happy and no one would have an incentive to defect and there would in fact be an equilibrium. But unfortunately, quite often, we fail to have coordination. Either everyone plays non-invest or, as happened the first time in class, we get some split with people losing money.?

A?party can be a coordination problem. One is the problem that if people don't show up it's a lousy party, so you don't want to show up. Conversely, if everyone is showing up, it's great, it's a lot of fun, it's the place to be and everyone wants to show up. Second--so there's two equilibria there, showing up and--everyone not showing up or everyone showing up. Similar idea, the location of parties which is what I thought you were driving at, but this similar idea can occur.?

The more people who use Microsoft and Microsoft programs, the bigger the advantage to me using Microsoft, and therefore--because I can exchange programs, I can exchange files if I'm working with my co-authors and so on, and so you can have different equilibria coordinating on different software, and again, you could end up at the wrong one. I think a lot of people would argue--but I'm going to stay neutral on this--a lot of people would argue that Microsoft wasn't necessarily the best place for the world to end up.?

How about political bandwagons? In politics, particularly in primaries, there may be advantage on the Democratic side or on the Republican side, in having you all vote for the same candidate in the primary, so they get this big boost and it doesn't seem like your party's split and so on. And that could end up--and again, I'm going to remain neutral on this--it just could end up with the wrong candidate winning. There's a political bandwagon effect, the person who wins New Hampshire and Iowa tends then to win everything, so that's another example.

What about bank runs? So you can imagine a bank as a natural case where there's two equilibria. There's a good equilibrium, everyone has confidence in the bank, everyone leaves their deposits in the bank. The bank is then able to lend some of that money out on a higher rate of interest on it. The bank doesn't want to keep all that money locked up in the vault. It wants to lend it out to lenders who can pay interest. That's a good equilibrium for everybody.?

However, if people lose confidence in the bank and start drawing their deposits out then the bank hasn't got enough cash in its vaults to cover those deposits and the bank goes under.?

So, what I want to do is, I want to pick on somebody in the class now--everyone understands this game, everyone understands there's two equilibria, everyone understands that one equilibrium is better. Let's play the game again. Let's choose the game again, but before I do I'm going to give the mike to Patrick here and Patrick is going to have exactly five seconds to persuade you. Stand up. Patrick's going to have five seconds to persuade you to tell you whatever he likes starting now.

So notice what happened here.?There's a lesson here; the lesson here is the game didn't change. It's the same game that we've played three times already. This was the fourth time we've played it. We had a totally different response in playing this time. Almost all of you, the vast majority of you, perhaps even 90% of you invested this time and you did so in response to Patrick. But Patrick wasn't putting any money down, he wasn't bribing you, he wasn't writing a contract with you, he wasn't threatening to break your legs, he just was pointing out it's a good idea.?

Now, remember the Prisoner's Dilemma, in the Prisoner's Dilemma, if Patrick could have got up in the Prisoner's Dilemma and given the same speech and said look guys, we're all better off if we choose β in the Prisoner's Dilemma than if we choose ?; roughly the same speech. What will you have done in the Prisoner's Dilemma? Nothing, we would end up in the bad outcome.

So, there's a lesson here, in coordination problems, unlike Prisoner's Dilemma, communication--just communication, no contracts--communication can help. And in particular, what we can persuade each other to do is to play the other Nash Equilibrium. Now, this gives us one more motivation for a Nash Equilibrium. In a Prisoner's Dilemma, to get out of it we needed a contract, we needed side payments, we needed to change the payoffs of the game.?

But a Nash Equilibrium can be a self-enforcing agreement. We can agree that we're going to play invest in this game, and indeed we will play invest without any side payments, without anybody threatening to break your leg, without any contracts, without any regulation or the law. We're going to end up doing the right thing here because it's in our own interest to do so. So coordination problems which we've agreed are all over society, whether it comes to bank runs or bubbles in the market, or fashion in the Midwest, they're all over society.?Communication can make a difference.