散文網(wǎng) » 科技 »學習 » [Geometry] Golden Ratio

[Geometry] Golden Ratio

2021-07-04 11:40 作者:AoiSTZ23 0人讀過 | 我要投稿

By: Tao Steven Zheng (鄭濤)

【Problem】

The golden ratio is a special ratio between two quantities in which the ratio between the two quantities is equal to the ratio of their sum to the larger of the two quantities. In modern mathematical notation:

$%5Cfrac%7Ba%7D%7Bb%7D%20%20%3D%20%5Cfrac%7Ba%2Bb%7D%7Ba%7D%20$

where $a%3Eb$ . Solve for the ratio $a%3Ab$ .

?

【Solution】

? $%5Cfrac%7Ba%7D%7Bb%7D%20%20%3D%20%5Cfrac%7Ba%2Bb%7D%7Ba%7D%20$

$a%5E2%3Db(a%2Bb)%0A$

$a%5E2%3Dba%2Bb%5E2%0A%0A$

$a%5E2-ba%3Db%5E2%0A$

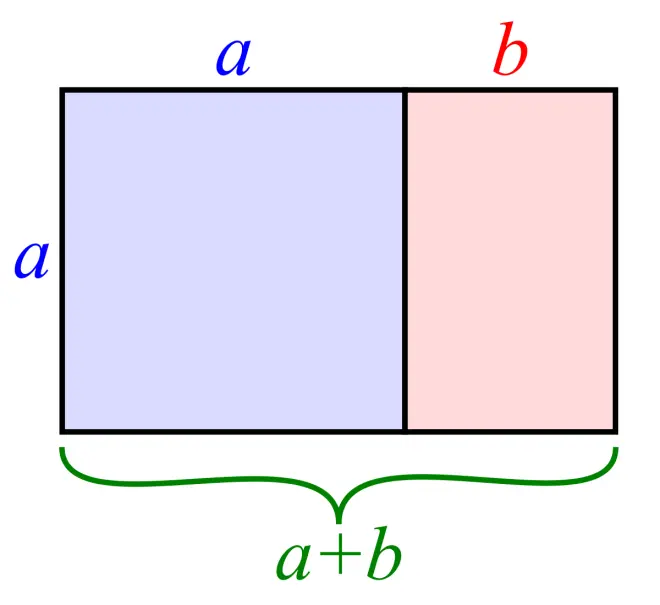
Solve for ? $a$ by completing the square.

$(a-b%2F2)%5E2%3Db%5E2%2B(b%2F2)%5E2%0A%0A$

$%0A(a-%5Cfrac%7Bb%7D%7B2%7D)%5E2%3D%5Cfrac%7B(5b)%5E2%7D%7B4%7D%0A$

Take the positive root (negative lengths are not permissible)

$a-%5Cfrac%7Bb%7D%7B2%7D%3D%5Cfrac%7B%5Csqrt%7B5%7D%20b%7D%7B2%7D%0A%0A$

$a%3D%5Cfrac%7B(1%2B%5Csqrt%7B5%7D)b%7D%7B2%7D%0A$

and obtain

$a%3Ab%3D%5Cfrac%7B1%2B%5Csqrt%7B5%7D%7D%7B2%7D%3A1$

標簽：