By: Tao Steven Zheng (鄭濤)

【Problem】

The following problem is from the Sunzi Suanjing (孫子算經(jīng)), a text written by an obscure mathematician with the surname Sun (name unknown) sometime around the 3rd to 5th centuries AD.

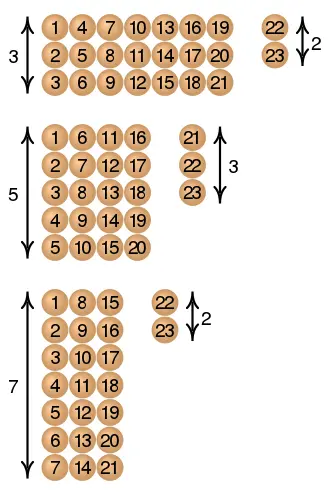
Suppose we have an unknown number of objects. When counted in threes,?2?are left over, when counted in fives,?3?are left over, and when counted in sevens,?2?are left over. How many objects are there?

[Assume the lowest positive integer solution]

【Solution】

This problem is a system of indeterminate equations with infinitely many solutions. According to the problem, we get

Calculate the product of the moduli

The solution of the Chinese remainder theorem prescribes that

For this problem

where

and? represent the modular inverses of each respective remainder.? The modular inverses can be solved systematically using Qin Jiushao's (大衍求一術(shù)) ; however, the numbers involved in this problem are small enough to be obtained by guessing and checking.

Final Calculation

Here, 233 is a solution, but this is not the lowest positive integer solution. The lowest positive integer solution is

So there are 23 objects.