【Calculus】Volume of the Bicylinder
By: Tao Steven Zheng (鄭濤)
【Problem】
The bicylinder
is a solid formed by intersecting two perpendicular cylinders of equal
cross-sections. The cross-sections of the intersecting cylinders are
circles of radius . Use integration to determine the volume of the bicylinder.
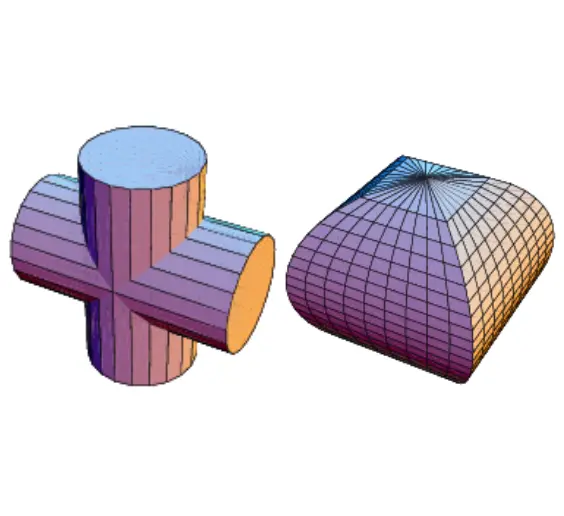

【Solution】
The first thing to consider are the level-curves in the direction of
integration. Let the integration be carried out in the x-axis. The
cross-sections in the x-axis are squares that vary under the constraint
of a circle with radius , which is the circle
. The side length the cross-sectional squares is given by the formula
Thus, the cross-sectional areas is the function

To determine the volume, integrate in the x-axis from one end of the circle to the other end.

