數(shù)學實現(xiàn)信號分析[ω]: 關于傅里葉的一些奇奇怪怪的捷徑

這篇就是傅里葉相關的最后一篇專欄了, 當然傅里葉遠不止這么點東西, 還有更多更多的知識等待被大家學習哦

FF.....FFFFFF
在高維傅里葉變換中, 其實有一個懶人計算方法
假設有一個n維函數(shù)(或序列), f(x1, x2, ..., xn), 那么整個傅里葉變換可以這樣算:
首先在x1方向對每一行進行一維傅里葉變換, 然后在x2方向再進行一次一維傅里葉變換, 以此類推, 最后在xn方向進行一次傅里葉變換
最后的結果與直接計算高維傅里葉變換的結果是一致的
證明:


F [f(r+r0)] (ω)
現(xiàn)實中總會遇到以下的情況: "已知有一個n維的函數(shù)f(或序列),?但是我們已知的起點是不在中心的(0, 0), 我們需要求出f經(jīng)過一段位移r0的傅里葉變換",?其中最常見的就是圖像變換, 我們理解的坐標原點是在圖像中心, 但是計算機理解的坐標原點是在圖像的左上角, 這時候就要進行相應的變換

同理, 逆變換也有相應的操作:

特別地, 需要注意一下, 在離散傅里葉變換中, 整個原序列 x 都是在n維的空間 [0, 1)^n 中, 但是經(jīng)過傅里葉變換后的頻率序列是在 [0, w)^n 中的
例子: 假如現(xiàn)在有一副100*200的圖片, 那么這副圖片所占用的空間為 [0, 1) * [0, 1), x方向兩點間隔為1/100, y方向兩點間隔為1/200; 而經(jīng)過傅里葉變換后的頻率序列占用的空間為 [0, 100) * [0, 200), x和y方向兩點的間隔都為1
?注意: 在離散傅里葉變換中, 使用這種方法進行位移的話會出現(xiàn) "循環(huán)位移" 的現(xiàn)象, 也就是說原版應該被移動到序列范圍外的數(shù)據(jù)點, 會再次出現(xiàn)在移動方向相反的地方, 例子:下面是一副744x906x3的圖片, 現(xiàn)在對這個圖片進行(400, 400)方向的位移, 得到結果:


卷積 Convolution
學神經(jīng)網(wǎng)絡的別興奮, 此卷積非彼卷積, 這個是數(shù)學上嚴格定義的卷積運算, 神經(jīng)網(wǎng)絡的卷積是因為和數(shù)學卷積類似才有了卷積這個名字而已
以下定義卷積運算:

卷積運算在工程上用處非常非常大, 只要選擇合適的核函數(shù)g, 在圖像方面可以用作模糊化, 在音頻方面可以用作降噪
但是在計算機中計算積分可不是一件容易的事情, 通常要等上幾十秒或者幾分鐘才可以出結果(這里用蛇py做例子), 于是就有了下面的快速計算方法:

證明:?(這里使用一維, 因為實在不想打字了, 寫公式好麻煩= =)


導數(shù)的傅里葉變換
f(t)的n階導數(shù)的傅里葉變換可以由以下方法求出:
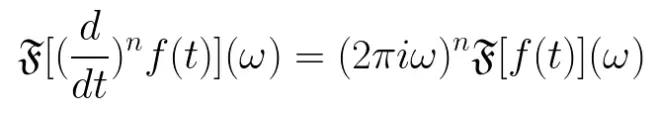
這里我只證明第一階求導, n階其實就是重復求導而已


Plancherel定理
在物理中經(jīng)常會提到系統(tǒng)的能量, 并且單一頻率的能量正比與這個頻率的平方
在傅里葉變換中存在保范性(因為還沒說過函數(shù)空間, 所以這里可以理解為能量守恒):

這也就是說變換前后的能量不會發(fā)生變化
證明:



關于分部積分:


