[Geometry] Inscribed Circle of a Triangle
By: Tao Steven Zheng (鄭濤)
【Problem】
The following problem is selected from Aida Yasuaki’s 《算法天生法指南》 (1811):
Suppose a circle is inscribed in a triangle with side lengths 13, 14, and 15. What is the diameter of the inscribed circle[1]?
[1] An inscribed circle is also called an incircle.

【Solution】
?(1) Use either Heron’s formula or Qin Jiushao’s formula for computing the area of a triangle.
Heron’s formula
Heron of Alexandria gave his formula in Book I of “Metrica”:
where ?is the area of a triangle with sides
,
,
and semi-perimeter
.
Qin Jiushao’s Formula
In the “Shushu Jiuzhang”《數(shù)書(shū)九章》, Qin Jiushao gave the formula:
where ?is the area of a triangle,
is the short side,
?is the middle side, and?
?is the long side. ?
?
(2)
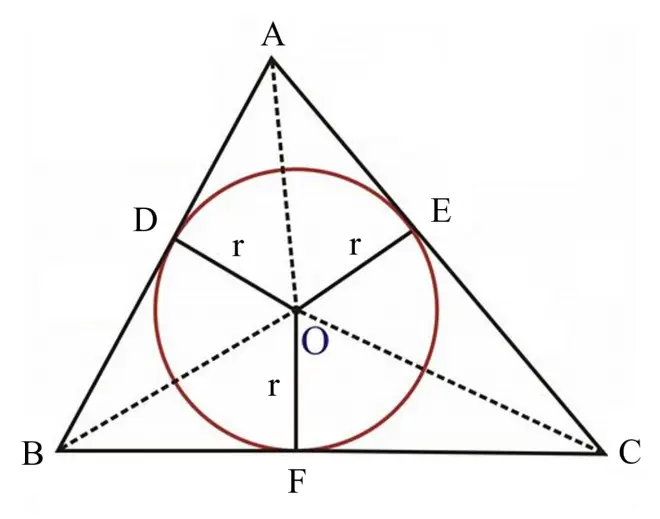
Figure 1 shows that ?can be split into three triangles:
, ?
and
. Hence, the area of
?is the sum
where
?Since the line segments ,
, and ?
are radii of the inscribed circle, let
. Let
,
, and
.
?Hence,
?
?Since the radius is half the diameter,
Therefore, the diameter of the inscribed circle is

