By: Tao Steven Zheng (鄭濤)

【Problem】

Omar Khayyam (1048 – 1131 AD) solved cubic equations of the form by transforming the problem into finding the intersection of a circle and a parabola:

where are positive numbers.

Part 1: Determine in terms of .
Part 2: Use Omar Khayyam’s method to solve the cubic equation by sketching the two conic sections and locating the intersection points.

【Solution】

Solution for Part 1
Write the first equation as and the second equation as . Substitute the second equation into the first equation to eliminate , and obtain .

Consequently,

or

Matching terms with the cubic equation gives

Since are positive numbers,

Solution for Part 2
For the equation , and . Thus,

and we need to graph

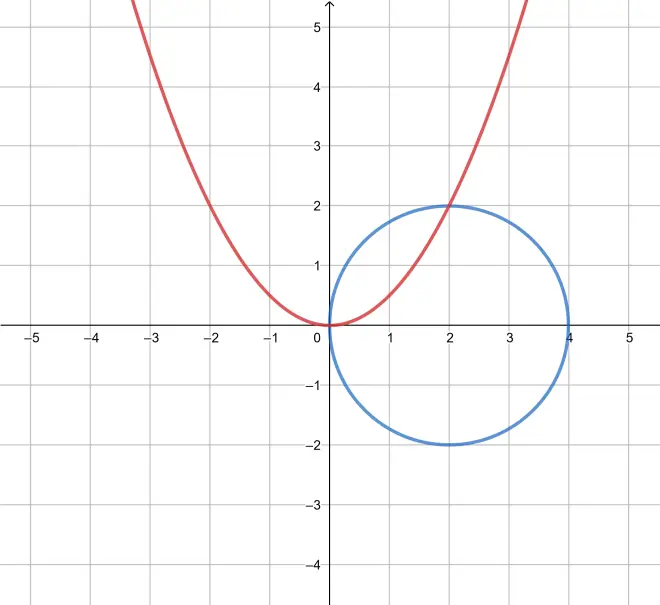
Intersection points: (0,0);? (2,2). When the values of is substituted into , we find only one solution to this cubic .