[Geometry] The Holey Cube
By: Tao Steven Zheng (鄭濤)
【Problem】
Here is a fun problem I came up in second year at UBC:
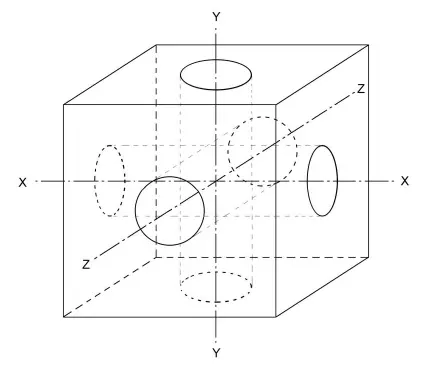
Imagine a cube with hole drilled through the centers of each face. Each hole is equal in size. We will call this solid the ''Holey Cube''. If the width of the cube is? and the radius of each hole is
, determine the volume of the Holey Cube.

Hint: Read these two articles first
【Calculus】Volume of the Bicylinder
【Calculus】Volume of the Tricylinder

【Solution】
The volume of the Holey Cube is not that simple to determine. It requires a bit of set theory, more specifically the inclusion-exclusion principle.
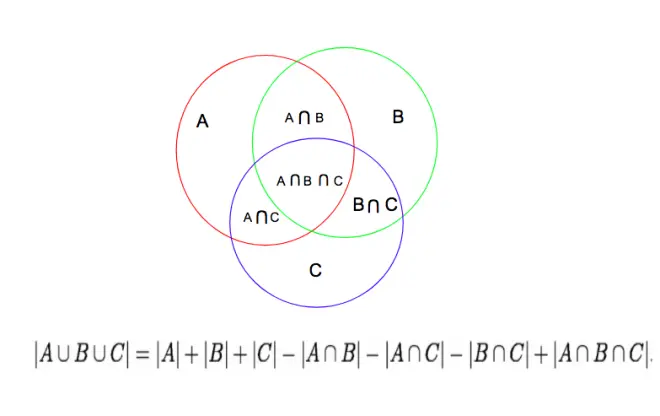
When the holes are drilled through the center of each face, we can see three cylinders taken out. But wait! What about the intersections of the cylindrical cavities? Since there are three cylinders (A, B, C), there are three bicylinders (AB, AC, BC) to patch up. But wait! What about the intersection of all three cylinders? Finally we need to remove a tricylinder (ABC).
Volume of the cube
Volume of the cylinder
Volume of the bicylinder
Volume of the tricylinder
Hence, the volume of the Holey Cube is

