GG 140: The Atmosphere, the Ocean, and Environmental Change

Lecture 03.?The Perfect Gas Law

https://oyc.yale.edu/geology-and-geophysics/gg-140/lecture-3

SI System of Units [00:00:00]

One we'll be using today also is the mass density. It's how much mass of a fluid or an object is there per unit volume. It's a mass per unit volume. So this is a really trivial one. There's no name for it, but it's going to be kilograms per meter cubed . Or kilograms, meter to the minus three.?So let me give you an example of that. The one we're going to be working on today is the perfect gas law. One way to write it is P equals rho (ρ) R T (P=ρRT). P is the pressure, rho (ρ) is the density, the mass density, R is the gas constant, and T is the temperature.

• Pressure is kilograms, meters to the minus one, seconds to the minus two. Now, that should be equal to the product of the units of all these other things. The units of mass density we've already said are kilograms per meter cubed.

• The units of the gas constant I'll give you. It's Joules per kilogram per degree Kelvin. And the temperature will be in Kelvins as well.

• Joule is kilogram, meter squared per second squared.?

Pressure and the Ideal Gas Law [00:09:55]

Let's first imagine a box full of gas molecules, but they're moving around. We know what the typical molecular speed is. They're colliding off each other, but they're also occasionally bouncing off the wall of that chamber.?And every time they do that, they impart a little bit of force to the wall that they bounce off of, and that's called pressure. It's the repeated bouncing of molecules off the side of a box that gives rise to this quantity we call pressure. It's going to depend, of course, on the number of molecules, their speed, and their mass, in principle. At least, it might depend on these things.

Now, if you've taken a course in chemistry, you probably have seen the perfect gas law written this way: pressure times volume equals n R T (PV=nRT). That's probably the most familiar way to write the perfect gas law in a chemistry course. Here, P is the pressure, V is the volume of the container that you have it in, n is the number of moles.?This is the gas constant. That's the temperature, of course, in Kelvins. That's the volume of the container. And that's the pressure.?A mole is a certain number of molecules. Avogadro's number--which is, if I remember, it's 6.02x10^23--is a number of molecules of any gas in a mole. So this would be the number of moles you have in that box.

The interesting thing about this formula is that it seems to be independent of the mass of the molecule. While I speculated that this might depend on the mass, it turns out that it doesn't depend on the mass. You would think that a molecule that has a heavier mass would impart more force as it bounces off the wall.?But you may remember from last time that at a given temperature, heavier molecules move more slowly. So in fact, those two factors cancel out in the perfect gas law. So the pressure you get depends only on the number of molecules that you have, not on the mass of those molecules.?

So I'm going to give you the form in which we will be using it in this class. Stop me if you have questions. We're going to write the perfect gas law as P=ρRT, where this is the pressure again, this is the mass density, that is the gas constant for the gas in question--we call it the specific gas constant, not the universal gas constant--and that again is the temperature in degrees Kelvin. The mass density is going to be the number of moles per unit volume times the molecular weight?(n/V). So the more molecules you have and the heavier each molecule is in a given volume, that's going to determine the mass density.?

We've defined the specific gas constant as being the universal gas constant divided by the molecular weight. We seem like we've made things more complicated, because we no longer have a universal gas constant. But we don't want to work in terms of number of molecules. We want to work in terms of the mass of the air.

For pressure, you should express it in Pascals. Or what is sometimes a more frequent unit in meteorology is a millibar. Millibar, which is sometimes written as a hectoPascal, which is 1/100 of?Pascals .In the meteorological literature, you'll often find hectoPascals used instead of Pascals.?

Buoyancy Force [00:20:39]

And there's a very simple idea that I'm sure you are aware of, and that is warm air rises, and cold air sinks. I'd like to actually prove that to you. And to do that, I'm going to have to define something called the buoyancy force. The buoyancy force is a pressure force on an object immersed in a liquid or a fluid in a gravity field.

As you go down in this fluid, the pressure's getting greater and greater. That means the pressure acting up on the bottom is greater than the pressure acting down on the top. So that's why I said it's got to be a liquid with some mass in a gravity field. Because only in a gravity field will there be that increase in pressure as you go down.?And that is what's causing this buoyancy force.?

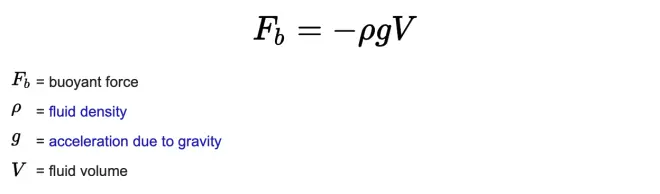
Archimedes' Law said that that buoyancy force is equal to the weight of the fluid displaced.?So in order to compute that force, we just have to know how much water would be there if the object were not there. In this case, it would be the volume of the object multiplied times the density of the fluid. But it's the weight, not the mass, so this has to be multiplied by little g, the acceleration of gravity. If you have something of mass m, its weight is the product of mass and the acceleration of gravity.?

Now, it's acting in the atmosphere all the time whenever you have a little parcel of air that's at a different temperature than its surroundings. And that's what I want to work out, and that's where the perfect gas law is going to be a very nice thing to have.

So I've worked out an example here. I've imagined a little piece of air-- maybe it's about this big-- that's got a certain pressure. I'm going to use the subscript p, because I'm calling this a parcel, a little parcel of air. It's got a density, and it's got a temperature. And then surrounding it is the environment. That'll be the pressure in the environment, the density of the environment, and the temperature of the environment. And my goal is to find out the buoyancy force acting on that parcel. I want to know, if it's warm, is it going to rise, or is it going to sink? And so on and so forth.

Now, we're going to have to make some assumptions, but they're going to be very good assumptions. The first assumption is we're going to assume that the pressure in the parcel is equal to the pressure of the environment. Why would that be? If you had air that was at different pressure than its environment, let's say at greater pressure, it would immediately expand until the pressure matched.

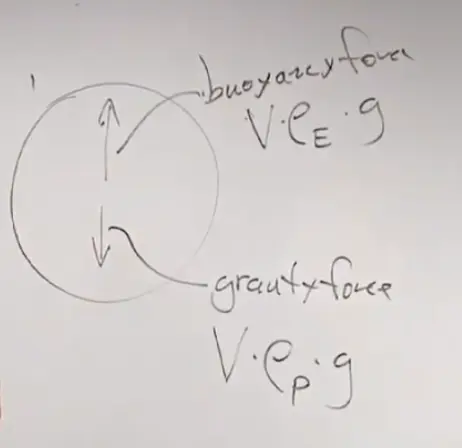
The buoyancy force acting up is going to be the volume--?we're using Archimedes' Law now, so it's?going to be this quantity here. It's going to be the volume again times the density of the environment-- that's the fluid that's been displaced-- times g.?The V's are the same for both, g is the same for both, but the densities appear differently.?The down force is related to the density of the parcel.?The up force is related to the density of the environment. If I had chosen a cooler temperature for the parcel, the parcel would be denser than air?and the parcel of air would sink.

This is probably the basic physics of what happens in the atmosphere to generate all the wind circulations, to generate clouds, sea breezes. Almost everything you can think of in the atmosphere, any air motion, probably can be tracked back to this simple little idea, that temperature differences, if the pressure is equilibrated, will generate buoyancy forces, either up or down.

Pressure is a force per unit area, and that's the thing that wants to equalize. There's no quick process-- temperature might equalize over an hour or two, because they're in contact with each other, but not that instantaneous equilibration like you get with a balloon popping. That's pressure equilibration, and it's fast and it's physical. And the other two either are slower, or just there's no tendency for that at all.

I can't leave this subject without mentioning mixtures of gases. So we imagine this same box, and it's got some A molecules, and it's got some B molecules. And they're all bouncing around off the walls and so on. There's a mixture of gas A and gas B. What is the deal there? When you mix two gasses together, what relationship do they have to each other??

The temperatures are going to quickly equilibrate. Even if the masses are different, because they're bouncing into each other frequently, thousands of times per second, the temperature of the A and B molecules will quickly come to the same value.

The pressure is additive. In other words, we can define the pressure that the A molecules are making, we can call that PA, and the pressure that the B molecules are making, that's PB. And the total pressure, PTotal, is just the sum of the two. So we use this term partial pressure--partial pressure of A, partial pressure of B--and they add up to give the total pressure.

When you're measuring pressure in a gas, you're measuring the sum of all the pressures of the components within that gas. Usually, we don't need to know that, but occasionally, that's the way we keep track of how much of these other gases you have. Someone might say, well, the partial pressure of water vapor is three millibars today or something like that. That's the contribution water vapor is making to the total pressure on this particular day.?

Composition of the Atmosphere [00:39:35]

Let me remind you what the atmospheric composition is for our atmosphere. For air on Earth, it's primarily nitrogen, oxygen, and argon. I'm going to give you the number two ways: by volume and?by mass.

For nitrogen, it's 78.1% by volume and 75.5% by mass. In other words, 78% of the molecules in this room are nitrogen, but 75.5% of the mass of the gas in this room is the nitrogen. Oxygen, 21.0% and 23.2%. Argon, 0.9% and 1.3%.

Just remember, there's this difference because the molecules have different masses. Some are heavier. Some are lighter. So whether you've counted up the molecules and are representing the fraction that way, or whether you're counting up the masses, you're going to get slightly different numbers for the two.

Now I've chosen, and the convention is to define that part as being the air, because these proportions are constant everywhere you go in the atmosphere. If I go to the North Pole, the Equator, the South Pole, if I go high in the atmosphere, winter or summer, these proportions are unchanging. So we call that air.

But then there are other gases as well. And sometimes they're called trace gases. Sometimes they're just called variable gases. They're found in varying proportions depending where you are. Let me give you an example. Probably the most important one is water, water vapor, H2O. And it's found anywhere from-- well, from let's say one part per 100, 10^-2, to really as small as you want to go, maybe 10^-5, by volume.

CO2, another very important gas, is more thoroughly mixed, but not perfectly mixed. A typical value these days might be about 395 parts per million by volume, ppmv. So we're using this method, we're counting molecules. I could write that as 395x10-6?by volume.?That varies only up and down by about 5%, plus or minus 5%. So that's nearly well mixed, but not quite as thoroughly mixed as these gases within the atmosphere-- within the air.

Some other molecules I mentioned last time on the slide you should be aware of are methane, nitrous oxide--N2O-- and ozone. And just be aware that those and a few other gases will pop up from time to time in this course, and we'll be wanting to know what their partial pressure is, what their mass ratio is, what their ratio by molecules is. We can convert back and forth between these different measures using the formulas that I've given you today.

Density and Pressure Variations with Altitude [00:45:36]

I think I may have time to do one other thing before we quit today then, and that's to talk about how density and pressure change with altitude. First of all, just some background information. The typical sea-level density, of course it varies from place to place. But if you want to work out a problem and you're not given enough information, you should know, for example, in this room, the density is about 1.2 kilograms per cubic meter. And a typical sea-level pressure is about 1,013 millibars or 1,013 two more zeros (101,300) Pascals. So let's take that as just basic climatological information.

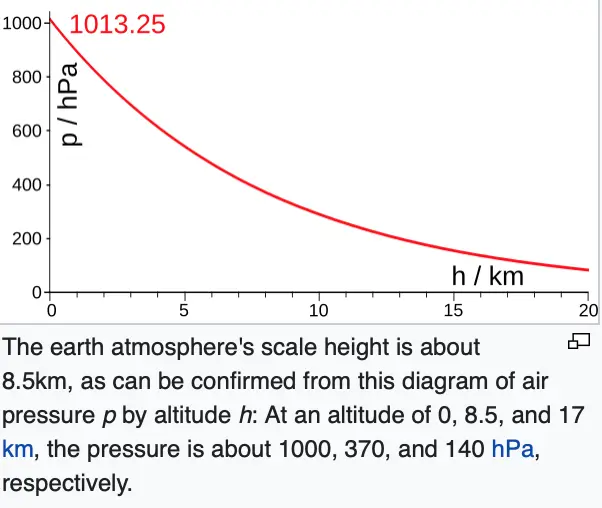
But now I'm interested in how those numbers change with height. Typically, if I plot pressure on the x-axis and height using the letter z on the y-axis, it looks like this. It decreases rapidly at first, then less rapidly, and so on, asymptotically, but never actually reaching zero. And if I plot air density, it looks very much the same.

It's such a simple relationship that we'd like to be able to have a formula for it. And there is a nice one, but we have to make an approximation now. We have to assume that the temperature is approximately constant with height, which is not a very good approximation, but we're looking here just to get a rough-- maybe an estimate at the 10% level or the 20% level, something in that range. But if this approximation is used, then I can write down a formula for the pressure as a function of height. It's the pressure at sea level times e to the minus z over Hs.

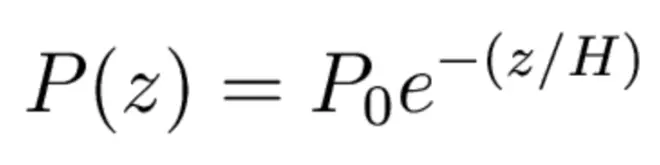
And there's a very simple formula for it. It's , the gas constant times the temperature divided by the surface gravity. Let's work it out for Earth. Air has a gas constant of 287. Let's take 288 for the temperature of the air and 9.81 for the acceleration of gravity. That turns out to be approximately 8,400 meters. Every time you go up 8,400 meters, you tick off another fractional decrease in atmospheric pressure and density.?At typical airliner flight level, the density and pressure that you're flying through is only about one quarter that you have here at sea level, and that's why the cabin has to be pressurized.