An Introduction to Modular Arithmetic
The best way to introduce modular arithmetic is to think of the face of a clock.
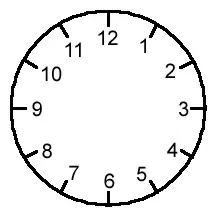
So?
13?becomes?1,?
14?becomes?2,?
and so on.
This can keep going, so when you get to "25?o'clock'', you are actually back round to where?1?o'clock is on the clock face (and also where?13?o'clock was too).
What we are saying is?
"13=1+?some multiple of?12", and?
"38=2+?some multiple of?12",?
or, alternatively, "the remainder when you divide?13?by?12?is?1" and "the remainder when you divide?38?by 12 is 2''. The way we write this mathematically is?
13≡1?mod?12,?
38≡2?mod?12
and so on. This is read as?
"13?is congruent to?1?mod (or modulo)?12" and?
"38?is congruent to?2?mod?12".

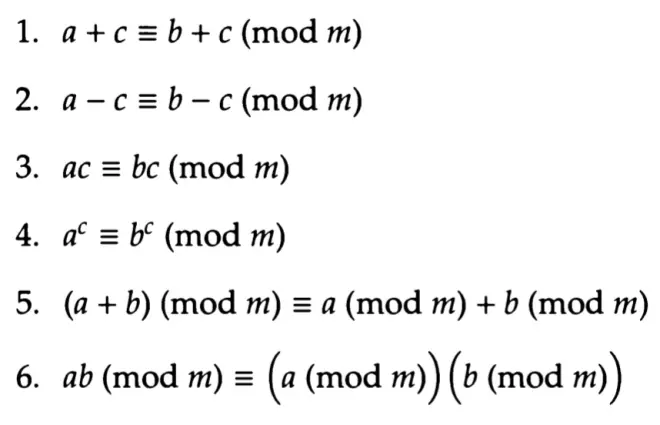

key words:
mod?u?lar?/?m?dj?l??$??mɑ?d??l?r/?adjective?
con?gru?ent?/?k??ɡru?nt?$??kɑ??-/?adjective
congruence
re?main?der?/r??me?nd??$?-?r/?●○○?noun