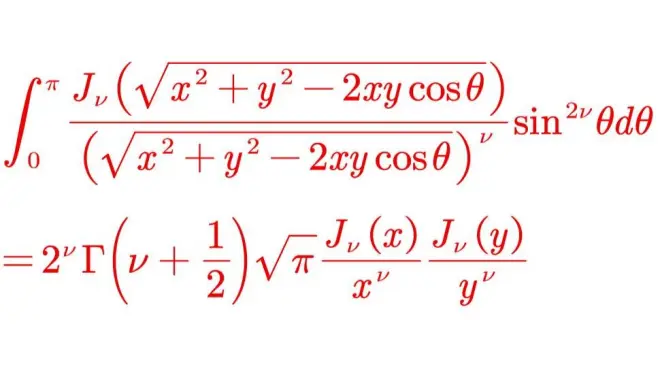
Sonine-Gegenbauer formula is an?important kind of finite integral involving?Bessel Functions.

It can be shown that

in which Z is?arbitrary?cylinder function (J, Y, H)

Above?formula holds when??for?any complex x≠0, y

We can deduce it from Gegenbauer addition formula, but this article will give?a new appraoch using contour integration.

A special case is?

Proof:

First, we can get a kind of integral expression of Bessel function from series expression of Bessel function and contour integral expression of Gamma function.

Hence, we can use contour integral?to express?following complicate function

Let ?denote the integral in the special case of Sonine-Gegenbauer formula, plug above expression?into , we obtain

Exchange the order of the double integral, and note that the integral nested in contour integral is?modified Bessel function of the first kind, hence

Denote?

Expand? and? into series, then change the summation order to 11,21,12,31,22,13,41,32,23,14..., we obtain

Note that the series which sum is from 0 to n is a?confluent hypergeometric function,?we can use?pffaf transform on it, then expand it?into series and exchange the order of summation and integration

Hence