Modular Arithmetic

Definition 5

?Let n ∈ N and let a,b ∈ Z. We say that a is congruent to b modulo n?

if n|(a?b).?

We write this as a ≡ b (mod n).

Theorem 2

Let n∈N and let a,b∈Z. TFAE：（"The Following Are Equivalent"）

1. a≡b(modn).
2. a and b leave the same remainder when divided by n.?

3. a=b+kn?for some?k∈Z.

Theorem 3

Let a1,a2,b1,b2 ∈ Z, and let n ∈ N.?

Suppose, further, that a1 ≡ a2 (mod?n) and b1 ≡b2 (mod?n). Then

1. a1 + b1 ≡ a2 + b2 (mod n).

2. a1b1 ≡ a2b2 (mod n).

3. a1 ? b1 ≡ a2 ? b2 (mod n).

Ok, this is pretty great, but it’s missing one operation! How do we perform division modulo n? Or even, can we?

As a reminder of how we defined division way back when, we had the following definition for the number 1/n?:

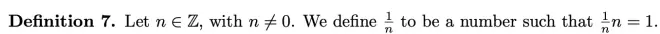
Definition 8

Let n ∈ N and let a ∈ Z. We say that u is?

if?au ≡ 1 (mod n).

So, in Example 8, we showed that 5 is a multiplicative inverse for 3 modulo 7.?

Let’s take a look at another example:

So sometimes inverses exist, and sometimes they don’t.?

There are common?factors between??6? and (2, 3, 4,6).

There are common?factors between? 7?and 7.

There are common?factors between? 8?and (2,4,6,8).

Examining the above 3 examples, you might notice a pattern: multiplicative inverses do not exist anytime the number we are interested in shares a factor with the modulus. This, in general, is the feature we are looking for.

Theorem 4.?

Let n ∈ N and a ∈ Z. Then a has a multiplicative inverse modulo n?

if and only if a ⊥ n.

example:

1?⊥ 6

5?⊥ 6

1?⊥ 7

2?⊥ 7

3?⊥ 7

4?⊥ 7

5?⊥ 7

6?⊥ 7

1?⊥ 8

3?⊥ 8

5?⊥ 8

7 ⊥ 8